ما هو الرقم 1 الذي يدل على أن المثلثات متساوية؟ العلامة الأولى لمساواة المثلثات. العلامة الثانية والثالثة لتساوي المثلثات. نسبة العناصر في المثلث القائم

مثلث . المثلثات الحادة والمنفرجة والقائمة.

الساقين والوتر. متساوي الساقين ومثلث متساوي الأضلاع.

مجموع زوايا المثلث.

الزاوية الخارجية للمثلث. علامات المساواة في المثلثات.

خطوط ونقاط رائعة في المثلث: الارتفاعات، المتوسطات،

منصفات، متوسطه متعامدين,

مركز الثقل، مركز الدائرة المحصورة، مركز الدائرة المنقوشة.

نظرية فيثاغورس. نسبة العرض إلى الارتفاع للمثلث التعسفي.

مثلث هو مضلع ذو ثلاثة جوانب (أو ثلاث زوايا). غالبًا ما يُشار إلى جوانب المثلث بأحرف صغيرة، والتي تتوافق مع الأحرف الكبيرة التي تشير إلى القمم المقابلة.

إذا كانت الزوايا الثلاث حادة ( شكل 20)، فهذا هو مثلث حاد الزوايا . إذا كان أحد الزوايا صحيحا(ج، الشكل 21)، إنه مثلث قائم; الجانبينأ، بتسمى تشكيل الزاوية اليمنى الساقين; جانبج، عكس زاوية مستقيمة، مُسَمًّى الوتر. إذا كان أحدزوايا منفرجة ( ب، الشكل 22)، إنه مثلث منفرج الزاوية.


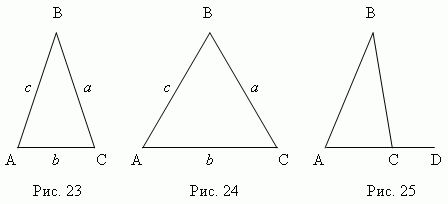
المثلث ABC (الشكل 23) - متساوي الساقين، لو اثنينجوانبها متساويةأ= ج); تسمى هذه الجوانب المتساوية جانبي، يتم استدعاء الطرف الثالث أساسمثلث. مثلث ABC (الشكل 24) - متساوي الاضلاع, لو الجميعجوانبها متساويةأ = ب = ج). على العموم ( أ ≠ ب ≠ ج) لدينا مختلف الأضلاعمثلث .

الخصائص الأساسية للمثلثات. في أي مثلث:

1. هناك زاوية أكبر مقابل الجانب الأكبر، والعكس صحيح.

2. الزوايا المتساوية تقع مقابل جوانب متساوية، والعكس صحيح.

وعلى وجه الخصوص، جميع الزوايا في متساوي الاضلاعالمثلثان متساويان.

3. مجموع زوايا المثلث هو 180 º .

ويترتب على الخاصيتين الأخيرتين أن كل زاوية متساوية الأضلاع

المثلث هو 60 º.

4. استمرار أحد أضلاع المثلث (أ، شكل 25)، نحن نحصل خارجي

زاوية بى سى دى . الزاوية الخارجية للمثلث تساوي مجموع الزوايا الداخلية،

لا علاقة لها :BCD=أ+ب.

5. أي ضلع المثلث أقل من مجموع الضلعين الآخرين فأكثر

خلافاتهم (أ < ب + ج, أ > ب – ج;ب < أ + ج, ب > أ – ج;ج < أ + ب,ج > أ – ب).

علامات المساواة في المثلثات.

يتطابق المثلثان إذا كانا متساويين على الترتيب:

أ ) الضلعان والزاوية بينهما؛

ب ) الزاويتان والجانب المجاور لهما؛

ج) ثلاثة جوانب.

علامات المساواة في المثلثات القائمة.

اثنين مستطيلييتطابق المثلثان إذا تحقق أحد الشروط التالية:

1) أرجلهم متساوية؛

2) الساق والوتر في أحد المثلثات يساويان الساق والوتر في المثلث الآخر؛

3) الوتر والزاوية الحادة لمثلث واحد يساوي الوتر والزاوية الحادة للمثلث الآخر؛

4) الساق والزاوية الحادة المجاورة لمثلث واحد تساوي الساق والزاوية الحادة المجاورة للمثلث الآخر؛

5) الساق والزاوية الحادة المقابلة لمثلث واحد متساويان مع الساق و مقابل الزاوية الحادة للآخر .

خطوط ونقاط رائعة في مثلث.

ارتفاع المثلث هوعمودي،يسقط من أي قمة إلى الجانب الآخر ( أو استمراره). ويسمى هذا الجانبقاعدة المثلث . الارتفاعات الثلاثة للمثلث تتقاطع دائمًافي نقطة واحدةمُسَمًّى مركز تقويم العظاممثلث. مركز تقويم المثلث الحاد (النقطةيا ، الشكل 26) يقع داخل المثلث، ومركز تقويم المثلث المنفرج (النقطةيا ، الشكل 27) – الخارج؛ يتطابق مركز تقويم المثلث الأيمن مع قمة الزاوية القائمة.

الوسيط - هذا القطعة المستقيمة - ربط أي رأس للمثلث بمنتصف الضلع المقابل. ثلاثة متوسطات للمثلث (AD، BE، CF، شكل 28) تتقاطع عند نقطة واحدة يا والذي يقع دائمًا داخل المثلثويكون له مركز الجاذبية. تقسم هذه النقطة كل وسيط بنسبة 2:1 من الأعلى.

منصف - هذا قطعة منصفةالزاوية من الأعلى إلى النقطة التقاطع مع الجهة المقابلة . ثلاثة منصفات المثلث (AD، BE، CF، شكل 29) تتقاطع عند نقطة واحدة أوه، دائما الاستلقاء داخل المثلثو كون مركز الدائرة المنقوشة(انظر القسم "مدرجوالمضلعات المقيدة).

يقسم المنصف الجانب المقابل إلى أجزاء تتناسب مع الجوانب المجاورة ; على سبيل المثال، في الشكل 29 AE : CE = AB : قبل الميلاد .

متوسط ​​عمودي هو عمودي مرسوم من المتوسطنقاط القطع (الجوانب). ثلاثة منصفات متعامدة للمثلث ABC(كو، مو، نو، الشكل 30 ) يتقاطعان عند نقطة واحدة O، وهي مركز دائرة مقيدة (النقاط K، M، N منتصف أضلاع المثلثاي بي سي).

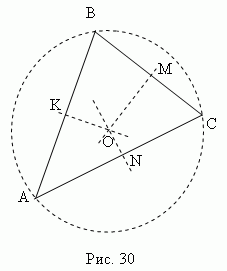
في المثلث حاد الزوايا، تقع هذه النقطة داخل المثلث؛ في منفرجة - في الخارج؛ في مستطيل - في منتصف الوتر. المركز المتعامد، مركز الجاذبية، مركز الدائرة المحصورة ومركز الدائرة المنقوشة تتطابق فقط في مثلث متساوي الأضلاع.

نظرية فيثاغورس. في المثلث القائم مربع الطولالوتر يساوي مجموع مربعات أطوال الساقين.

من الواضح أن إثبات نظرية فيثاغورس يأتي من الشكل 31. فكر في مثلث قائم الزاوية ABC مع الساقين أ، بوالوتر ج.

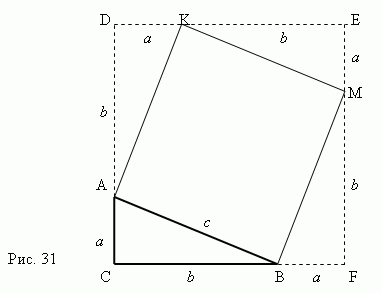
دعونا نبني مربعاأكمب باستخدام الوترأ.ب كجانب. ثمتمديد جوانب المثلث الأيمناي بي سي حتى تحصل على مربع CDEF ، الذي يساوي جانبهأ + ب .الآن أصبح من الواضح أن مساحة المربع CDEF هو ( أ + ب) 2 . ومن ناحية أخرى هذا المنطقة تساوي المبلغالمناطق أربعة مثلثات قائمةومربع AKMB ، وهذا هو

ج 2 + 4 (أب / 2) = ج 2 + 2 أب,

من هنا،

ج 2 + 2 أب= (أ + ب) 2 ,

وأخيرا لدينا:

ج 2 =أ 2 +ب 2 .

نسبة العرض إلى الارتفاع للمثلث التعسفي.

في الحالة العامة (للمثلث التعسفي) لدينا:

ج 2 =أ 2 +ب 2 – 2أب· كوس ج،

أين سي - الزاوية بين الجانبينأو ب .

يقال إن مثلثان متطابقان إذا أمكن جمعهما بالتداخل. يوضح الشكل 1 المثلثين المتساويين ABC و A 1 B 1 C 1. ويمكن فرض كل من هذه المثلثات على الآخر بحيث تكون متوافقة تماما، أي أن رؤوسها وأضلاعها متوافقة في أزواج. ومن الواضح أن زوايا هذه المثلثات سوف تتطابق أيضًا في أزواج.

وبالتالي، إذا كان مثلثان متطابقين، فإن عناصر (أي الجوانب والزوايا) لأحد المثلثين تكون متساوية على التوالي مع عناصر المثلث الآخر. لاحظ أن في مثلثات متساوية مقابل أضلاع متساوية(أي، متداخلة عند فرضه) زوايا متساوية تكمنوالعودة: الجوانب المتساوية تقع مقابل زوايا متساوية على التوالي.

لذلك، على سبيل المثال، في المثلثات المتساوية ABC و A 1 B 1 C 1، الموضحة في الشكل 1، فإن الجانبين المتساويين AB و A 1 B 1، على التوالي، يقعان في زاويتين متساويتين C و C 1. سنشير إلى تساوي المثلثين ABC و A 1 B 1 C 1 على النحو التالي: Δ ABC = Δ A 1 B 1 C 1. اتضح أنه يمكن إثبات تساوي المثلثين من خلال مقارنة بعض عناصرهما.

النظرية 1. العلامة الأولى لمساواة المثلثات.إذا كان ضلعان والزاوية بينهما لمثلث واحد متساويان على التوالي مع ضلعين والزاوية بينهما لمثلث آخر، فإن هذه المثلثات تكون متطابقة (الشكل 2).

دليل. خذ بعين الاعتبار المثلثين ABC و A 1 B 1 C 1، حيث AB = A 1 B 1، AC = A 1 C 1 ∠ A = ∠ A 1 (انظر الشكل 2). لنثبت أن Δ ABC = Δ A 1 B 1 C 1 .

بما أن ∠ A = ∠ A 1، فيمكن تركيب المثلث ABC على المثلث A 1 B 1 C 1 بحيث تتم محاذاة الرأس A مع الرأس A 1، ويتم تركيب الجانبين AB وAC على التوالي على الشعاعين A 1 B 1 وA 1. ج1 . بما أن AB = A 1 B 1، AC = A 1 C 1، فإن الجانب AB سوف يتماشى مع الجانب A 1 B 1 والجانب AC سوف يتماشى مع الجانب A 1 C 1؛ على وجه الخصوص، ستتزامن النقاط B وB 1 وC وC 1. وبالتالي، سيتم محاذاة الجانبين BC وB 1 C 1. لذا، المثلثان ABC و A 1 B 1 C 1 متوافقان تمامًا، مما يعني أنهما متساويان.

تم إثبات النظرية 2 بطريقة مماثلة باستخدام طريقة التراكب.

النظرية 2. العلامة الثانية لمساواة المثلثات.إذا كان ضلع وزاويتان متجاورتان لمثلث واحد متساويان على التوالي مع ضلع وزاويتين متجاورتين لمثلث آخر، فإن هذه المثلثات تكون متطابقة (الشكل 34).

تعليق. بناءً على النظرية 2، تم إنشاء النظرية 3.

النظرية 3. مجموع أي زاويتين داخليتين في المثلث أقل من 180 درجة.

النظرية 4 تتبع من النظرية الأخيرة.

النظرية 4. الزاوية الخارجية للمثلث أكبر من أي زاوية داخلية غير مجاورة لها.

النظرية 5. العلامة الثالثة لمساواة المثلثات.إذا كانت ثلاثة أضلاع لمثلث واحد متساوية على التوالي مع ثلاثة أضلاع لمثلث آخر، فإن هذه المثلثات متطابقة ().

مثال 1.في المثلثين ABC و DEF (الشكل 4)

∠ A = ∠ E، AB = 20 سم، AC = 18 سم، DE = 18 سم، EF = 20 سم، قارن بين المثلثين ABC وDEF. ما الزاوية في المثلث DEF التي تساوي الزاوية B؟

حل. وهذه المثلثات متساوية حسب الإشارة الأولى. الزاوية F للمثلث DEF تساوي الزاوية B للمثلث ABC، نظرًا لأن هاتين الزاويتين تقعان مقابل ضلعين متساويين على التوالي DE وAC.

مثال 2.يتقاطع المقطعان AB وCD (الشكل 5) عند النقطة O، التي تقع في منتصف كل منهما. ما هو طول القطعة BD إذا كان القطعة AC 6 م؟

حل. المثلثان AOC وBOD متساويان (وفقًا للمعيار الأول): ∠ AOC = ∠ BOD (عموديًا)، AO = OB، CO = OD (حسب الحالة).
ويترتب على تساوي هذه المثلثات أن أضلاعها متساوية، أي AC = BD. ولكن بما أنه وفقًا للشرط AC = 6 م، فإن BD = 6 م.

في هذا الدرس سوف ندرس العلامة الأولى لتساوي المثلثات. أولا، نقوم بصياغة وإثبات نظرية المعيار الأول لتساوي المثلثات. بعد ذلك، سنحل المسائل باستخدام العلامة الأولى لتساوي المثلثات.

في الدرس السابق، قدمنا ​​مفهوم "المثلثات المتساوية" - المثلثات التي يمكن دمجها عن طريق التداخل. ومع ذلك، من الصعب جدًا مقارنة الأشكال حسب التعريف، لذلك سنقدم معايير مساواة المثلثات - حسب بعض العناصر.

أرز. 1. المثلثان ABC و A 1 B 1 C 1 متساويان

دعونا نثبت النظرية: إذا كان الضلعان والزاوية بينهما في مثلث واحد والضلعين المقابلين والزاوية بينهما في المثلث الثاني متساويان، فإن هذين المثلثين متطابقان.

نظرية: نظرا. إثبات : ABC و .

الدليل: دعونا نتراكب البيانات في حالة الأشكال. نتيجة لهذا الإجراء، تتطابق القمم A و A 1 والقطاعات AB و A 1 B 1 و AC و A 1 C 1. إذا نظرنا إلى المثلثات ككل، فسوف تتطابق مع .

لقد تم إثبات النظرية.

دعونا ننظر في العديد من المشاكل.

يتم تقسيم القطع AC و BD إلى النصف عند نقطة تقاطعهما O. اثبت ذلك .

الدليل: لنقم بعمل رسم توضيحي.

أرز. 2. الرسم على سبيل المثال 1

لاحظ أن الزاويتين AOB وCOD متساويتان، مثل الزوايا الرأسية، وأن الجانبين BO وAO للمثلث AOB متساويان على التوالي مع الجانبين OD وOC للمثلث COD. ولذلك فإن المثلثين AOB و COD متساويان حسب المعيار الأول.

يتم تقسيم القطع AC وBD إلى النصف عند نقطة التقاطع. اثبت ذلك .

أرز. 3. الرسم على سبيل المثال 2

وفي المسألة السابقة أثبتنا ذلك حسب الإشارة الأولى. من هذه الاعتبارات يمكننا أن نستنتج أن AB = CD، ∠OAB = ∠OCD.

الآن دعونا نلقي نظرة على المثلثات . لديهم AC - جانب مشترك، AB = CD، و∠CAB = ∠ACD (كما ثبت). لذلك، وفقا لأول علامة على المساواة. Q.E.D.

أرز. 4. الرسم على سبيل المثال 3

في الشكل 3، القطع AB وAC متساوية. الزاوية 1 تساوي الزاوية 2 ومن المعروف أن AC = 15 سم، DC = 5 سم، أثبت ذلك. أوجد أطوال القطع BD وAB.

المثلثان متساويان حسب المعيار الأول، لأن ∠1 = ∠2، AB = AC، وAD هو الضلع المشترك للمثلثين. ويترتب على تساوي المثلثات أن بعض العناصر المتناظرة فيها متساوية، وبالتالي: BD = CD = 5 cm،

AB = AC = 15 سم.

الجواب: 5 سم، 15 سم.

في الشكل 5 قبل الميلاد = م. الزاوية 1 تساوي الزاوية 2 AD = 17 سم CD = 14 سم أثبت ذلك . ابحث عن AB وBC.

أرز. 5. الرسم على سبيل المثال 4

المثلث ABC يساوي المثلث CDA. وفقا للعلامة الأولى. ∠1 = ∠2، CB = AD، وAC هو الضلع المشترك لكلا المثلثين. إنه يتبع هذا ، .

1. موضوع الدرس "العلامة الأولى لمساواة المثلثات"
2. مثلث. الدليل

1. رقم 36. بوتوزوف ف.ف.، كادومتسيف إس.بي.، براسولوفا ف.ف. الهندسة 7 / ف.ف. بوتوزوف، س. كادومتسيف ، ف. براسولوفا، أد. سادوفنيتشيغو ف. - م: التربية، 2010.

2. أثبت أن المثلثين BOA وEOC متطابقان. يتم تقسيم القطع BE وAC إلى النصف حسب نقطة تقاطعهما.

3. أثبت أن الخط المستقيم الذي يقطع قطعاً متساوية من أضلاع زاوية يكون عمودياً على منصفها.

4. * تم رسم القطعتين المتساويتين MA وMC على جانبي الزاوية M وتم رسم منصفها ووضع علامة على النقطة B. أثبت أن BM هو منصف الزاوية ABC.

تذكرة 2

السؤال رقم 1

اختبارات تساوي المثلثات (إثبات الكل)

العلامة الأولىتساوي المثلثين : في الضلعين والزاوية بينهما ( نظرية 3.1. – علامة تساوي المثلثين بين ضلعين والزاوية بينهما - إذا كان الضلعان والزاوية بينهما لمثلث واحد متساويان على التوالي مع ضلعين والزاوية بينهما لمثلث آخر، فإن هذه المثلثات متطابقة)

دليل:

لنفترض أن المثلثين ABC و A 1 B 1 C 1 لهما زاوية A تساوي الزاوية A 1، AB تساوي A 1 B 1، AC تساوي A 1 C 1، فلنثبت أن المثلثين متساويان.

نظرًا لأن A 1 B 1 يساوي A 1 B 2، فإن الرأس B 2 سوف يتزامن مع B 1. وبما أن الزاوية B 1 A 1 C 1 تساوي الزاوية B 2 A 1 C 2، فإن الشعاع A 1 سيتزامن C 2 مع A 1 C 1 . بما أن A 1 C 1 يساوي A 1 C 2، فإن C 2 سوف يتطابق مع C 1. وهذا يعني أن المثلث A 1 B 1 C 1 يتطابق مع المثلث A 1 B 2 C 2، مما يعني أنه يساوي المثلث ABC.

لقد تم إثبات النظرية.

الثاني لافتةمساواة المثلثات: على طول الجوانب والزوايا المجاورة (نظرية 3.2. - علامة تساوي المثلثات حسب الجوانب والزوايا المجاورة - إذا كان أحد الجوانب والزوايا المجاورة لمثلث واحد متساويًا على التوالي مع الجوانب والزوايا المجاورة لمثلث آخر، فإن هذه المثلثات متطابقة)

دليل:

يترك ABC و A 1 B 1 C 1 هما مثلثان، حيث AB تساوي A 1 B 1، والزاوية A تساوي الزاوية A 1، والزاوية B تساوي الزاوية B 1. دعونا نثبت أنهم متساوون.

لنفترض أن A 1 B 2 C 2 مثلث يساوي ABC، ويكون رأسه B 2 على الشعاع A 1 B 1 ورأسه C 2 في نفس نصف المستوى بالنسبة إلى الخط المستقيم A 1 B 1، حيث يقع الرأس C 1.

نظرًا لأن A 1 B 2 يساوي A 1 B 1، فإن قمة B 2 ستتزامن مع B 1. نظرًا لأن الزاوية B 1 A 1 C 2 تساوي الزاوية B 1 A 1 C 1 والزاوية A1B1C2 تساوي الزاوية A1B1C1، فإن الشعاع A 1 C 2 سيتزامن مع A 1 C 1، والشعاع B 1 C 2 سيتزامن مع B 1 C 1. ويترتب على ذلك أن الرأس C 2 يتزامن مع C 1. وهذا يعني أن المثلث A 1 B 1 C 1 يتطابق مع المثلث A 1 B 2 C 2، مما يعني أنه يساوي المثلث ABC.

لقد تم إثبات النظرية.

الثالث لافتةمساواة المثلثات: من ثلاثة جوانب (نظرية 3.6. -) اختبار تساوي المثلثات في ثلاثة أضلاع - إذا كانت ثلاثة أضلاع لمثلث واحد متساوية مع ثلاثة أضلاع لمثلث آخر، فإن هذه المثلثات متطابقة)

دليل:

يترك ABC و A 1 B 1 C 1 هما مثلثان حيث AB يساوي A 1 B 1، AC يساوي A 1 C 1، و BC يساوي B 1 C 1. دعونا نثبت أنهم متساوون.

لنفترض أن المثلثين غير متساويين. إذن فإن زاويتهم A لا تساوي الزاوية A 1، والزاوية B لا تساوي الزاوية B 1، والزاوية C لا تساوي الزاوية C 1. وإلا لكانوا متساوين، على أساس الريش.

لنفترض أن A 1 B 1 C 2 مثلث يساوي المثلث ABC، الذي يقع رأسه C 2 في نفس نصف المستوى مع قمة C 1 بالنسبة إلى الخط المستقيم A 1 B 1.

دع D تكون نقطة منتصف القطعة C 1 C 2. المثلثان A 1 C 1 C 2 و B 1 C 1 C 2 متساويان الساقين وقاعدتهما مشتركة C 1 C 2. لذلك، فإن متوسطاتها A 1 D و B 1 D هي ارتفاعات، مما يعني أن الخطوط A 1 D و B 1 D متعامدة مع الخط C 1 C 2. الخطان A 1 D و B 1 D لا يتطابقان، لأن النقطتين A 1، B 1 , D لا يقعان على نفس الخط، ولكن من خلال النقطة D من الخط C 1 C 2 يمكن رسم خط واحد عمودي عليها فقط. لقد وصلنا إلى التناقض.

من بين العدد الهائل من المضلعات، والتي هي في الأساس عبارة عن خط مغلق وغير متقاطع، فإن المثلث هو الشكل ذو الزوايا الأقل. وبعبارة أخرى، هذا هو أبسط مضلع. ولكن، على الرغم من كل بساطته، فإن هذا الرقم محفوف بالعديد من الألغاز والاكتشافات المثيرة للاهتمام، والتي تضيء فرع خاص من الرياضيات - الهندسة. يبدأ تدريس هذا التخصص في المدارس من الصف السابع، ويحظى موضوع "المثلث" هنا باهتمام خاص. لا يتعلم الأطفال القواعد المتعلقة بالشكل نفسه فحسب، بل يقارنونها أيضًا من خلال دراسة العلامات الأولى والثانية والثالثة لمساواة المثلثات.

أول لقاء

إحدى القواعد الأولى التي يتعلمها تلاميذ المدارس هي كالتالي: مجموع قيم جميع زوايا المثلث يساوي 180 درجة. لتأكيد ذلك، يكفي استخدام المنقلة لقياس كل من القمم وجمع كل القيم الناتجة. وعلى هذا فإنه بوجود كميتين معلومتين يسهل تحديد الثالثة. على سبيل المثال: في مثلث قياس إحدى الزاويتين 70 درجة والأخرى 85 درجة، ما قياس الزاوية الثالثة؟

180 - 85 - 70 = 25.

الجواب: 25 درجة.

يمكن أن تكون المشكلات أكثر تعقيدًا إذا تم تحديد قيمة زاوية واحدة فقط، وتم إخبار القيمة الثانية فقط بمقدار أو عدد المرات التي تكون فيها أكبر أو أصغر.

في المثلث، لتحديد بعض معالمه، يمكن رسم خطوط خاصة، لكل منها اسمه الخاص:

• الارتفاع - خط مستقيم عمودي مرسوم من قمة الرأس إلى الجانب الآخر؛
• تتقاطع الارتفاعات الثلاثة، المرسومة في وقت واحد، في وسط الشكل، وتشكل مركز تقويم العظام، والذي، اعتمادًا على نوع المثلث، يمكن وضعه في الداخل والخارج؛
• الوسيط - الخط الذي يربط قمة الرأس بمنتصف الجانب الآخر؛
• تقاطع المتوسطات هو نقطة جاذبيتها الموجودة داخل الشكل؛
• منصف - خط يمتد من قمة الرأس إلى نقطة التقاطع مع الجانب المقابل، ونقطة تقاطع ثلاثة منصفات هي مركز الدائرة المنقوشة.

حقائق بسيطة عن المثلثات

المثلثات، مثل جميع الأشكال، لها خصائصها وخصائصها الخاصة. كما ذكرنا سابقًا، هذا الشكل هو أبسط مضلع، ولكن له سماته المميزة:

• الزاوية ذات القيمة الأكبر تقع دائمًا مقابل الضلع الأطول، والعكس صحيح؛
• الزوايا المتساوية تقع مقابل جوانب متساوية، مثال على ذلك المثلث المتساوي الساقين؛
• مجموع الزوايا الداخلية يساوي دائمًا 180 درجة، وهو ما تم إثباته بالفعل بالمثال؛
• عندما يمتد أحد أضلاع المثلث إلى ما هو أبعد من حدوده يتكون الزاوية الخارجيةوالتي ستكون دائمًا مساوية لمجموع الزوايا غير المجاورة لها؛
• يكون أحد الجانبين دائمًا أقل من مجموع الجانبين الآخرين، ولكنه أكبر من الفرق بينهما.

أنواع المثلثات

المرحلة التالية من التعارف هي تحديد المجموعة التي ينتمي إليها المثلث المعروض. الانتماء إلى نوع أو آخر يعتمد على حجم زوايا المثلث.

• متساوي الساقين - مع جانبين متساويين، يسمى الجانبي، والثالث في هذه الحالة بمثابة قاعدة الشكل. الزوايا الموجودة في قاعدة هذا المثلث هي نفسها، والوسيط المرسوم من الرأس هو المنصف والارتفاع.
• المثلث المنتظم أو متساوي الأضلاع هو المثلث الذي تكون جميع أضلاعه متساوية.
• المستطيل: قياس إحدى زواياه 90 درجة. في هذه الحالة، يسمى الجانب المقابل لهذه الزاوية الوتر، ويسمى الجانبان الآخران الساقين.
• مثلث حاد الزوايا - جميع زواياه أقل من 90 درجة.
• منفرجة - إحدى الزوايا التي يزيد قياسها عن 90 درجة.

المساواة والتشابه في المثلثات

أثناء عملية التعلم، لا يأخذون بعين الاعتبار شكلًا واحدًا فحسب، بل يقارنون أيضًا مثلثين. وهذا الموضوع الذي يبدو بسيطًا يحتوي على الكثير من القواعد والنظريات التي يمكن من خلالها إثبات أن الأشكال المعنية هي مثلثات متساوية. معايير مساواة المثلثات لها التعريف التالي: المثلثات متساوية إذا كانت أضلاعها وزواياها المتناظرة هي نفسها. مع هذه المساواة، إذا قمت بتركيب هذين الشكلين فوق بعضهما البعض، فإن جميع خطوطهما سوف تتقارب. أيضًا، يمكن أن تكون الأشكال متشابهة، على وجه الخصوص، ينطبق هذا على الأشكال المتطابقة تقريبًا والتي تختلف فقط في الحجم. من أجل التوصل إلى مثل هذا الاستنتاج حول المثلثات المعروضة، يجب استيفاء أحد الشروط التالية:

• زاويتان من شكل واحد تساوي زاويتين من شكل آخر؛
• يتناسب ضلعا أحدهما مع ضلعي المثلث الثاني، وتكون الزوايا المتكونة من الجانبين متساوية؛
• ثلاثة جوانب من الشكل الثاني هي نفس الأول.

بالطبع، من أجل المساواة التي لا جدال فيها والتي لن تثير أدنى شك، من الضروري أن يكون لديك نفس القيم لجميع عناصر كلا الشكلين، ومع ذلك، مع استخدام النظريات، يتم تبسيط المهمة إلى حد كبير، وعدد قليل فقط الشروط المسموح بها لإثبات تساوي المثلثات.

العلامة الأولى لمساواة المثلثات

يتم حل المسائل في هذا الموضوع بناءً على إثبات النظرية التي تقول: “إذا كان ضلعان في مثلث والزاوية التي يشكلانها متساويان مع ضلعين وزاوية مثلث آخر، فإن الأشكال أيضًا تساوي ضلعين وزاوية مثلث آخر”. بعضها البعض."

كيف يبدو إثبات نظرية العلامة الأولى لتساوي المثلثات؟ يعلم الجميع أن القطعتين متساويتان إذا كان لهما نفس الطول، أو أن الدوائر متساوية إذا كان لهما نفس نصف القطر. وفي حالة المثلثات، هناك العديد من العلامات، والتي يمكننا أن نفترض أن الأشكال متطابقة، وهي مريحة للغاية للاستخدام عند حل المهام الهندسية المختلفة.

كيف تبدو نظرية "العلامة الأولى لمساواة المثلثات" موصوفة أعلاه، ولكن هنا دليلها:

• لنفترض أن المثلثين ABC و A 1 B 1 C 1 لهما نفس الجوانب AB و A 1 B 1، وبالتالي BC و B 1 C 1، والزوايا التي تشكلها هذه الجوانب لها نفس الحجم، أي أنها متساوية. ثم، من خلال تركيب △ ABC على △ A 1 B 1 C 1، نحصل على تطابق جميع الخطوط والقمم. ويترتب على ذلك أن هذه المثلثات متطابقة تمامًا، وبالتالي فهي متساوية مع بعضها البعض.

نظرية "العلامة الأولى لتساوي المثلثات" تسمى أيضًا "على الجانبين والزاوية". في الواقع، هذا هو جوهرها.

نظرية حول العلامة الثانية

ويتم إثبات علامة المساواة الثانية بطريقة مماثلة؛ فالبرهان يعتمد على حقيقة أنه عندما يتم تركيب الأشكال على بعضها البعض، فإنها تتطابق تمامًا من جميع القمم والجوانب. ويبدو أن النظرية هي كما يلي: "إذا كان جانب واحد وزاويتان في التكوين الذي يشارك فيه يتوافقان مع جانب وزاويتين للمثلث الثاني، فإن هذه الأشكال متطابقة، أي متساوية".

العلامة الثالثة والبرهان

إذا كانت كلتا علامتي تساوي المثلثات 2 و 1 تتعلقان بجوانب الشكل وزواياه، فإن الإشارة الثالثة تشير إلى الجوانب فقط. لذا، فإن النظرية لها الصيغة التالية: "إذا كانت جميع أضلاع مثلث واحد تساوي ثلاثة أضلاع للمثلث الثاني، فإن الأشكال متطابقة".

لإثبات هذه النظرية، نحتاج إلى الخوض في تعريف المساواة بمزيد من التفصيل. في الأساس، ماذا تعني عبارة "المثلثات متساوية"؟ تقول الهوية أنه إذا قمت بتركيب شكل على آخر، فإن جميع عناصره ستتطابق، ولا يمكن أن يكون هذا هو الحال إلا عندما تكون أضلاعه وزواياه متساوية. وفي الوقت نفسه، فإن الزاوية المقابلة لأحد الأضلاع، والتي هي نفس زاوية المثلث الآخر، ستكون مساوية للرأس المقابل في الشكل الثاني. تجدر الإشارة إلى أنه في هذه المرحلة يمكن بسهولة ترجمة الدليل إلى معيار واحد لمساواة المثلثات. إذا لم يتم ملاحظة مثل هذا التسلسل، فإن المساواة بين المثلثات مستحيلة ببساطة، إلا في الحالات التي يكون فيها الشكل صورة مرآة للأول.

المثلثات الصحيحة

يحتوي هيكل هذه المثلثات دائمًا على رؤوس بزاوية 90 درجة. ولذلك فإن العبارات التالية صحيحة:

• المثلثات ذات الزوايا القائمة متساوية إذا كانت أرجل أحدهما متطابقة مع أرجل الثاني؛
• يكون الشكلان متساويين إذا كانت الوتر وأحد أرجلهما متساويتين؛
• تكون هذه المثلثات متطابقة إذا كانت أرجلها والزاوية الحادة متطابقة.

تشير هذه العلامة إلى أنه لإثبات النظرية يتم تطبيق تطبيق الأشكال على بعضها البعض، ونتيجة لذلك يتم طي المثلثات بواسطة الأرجل بحيث يخرج خطان مستقيمان مع الجانبين CA و CA 1.

الاستخدام العملي

في معظم الحالات، في الممارسة العملية، يتم استخدام العلامة الأولى لمساواة المثلثات. في الواقع، يتم استخدام موضوع الصف السابع الذي يبدو بسيطًا في الهندسة والتخطيط أيضًا لحساب طول كابل الهاتف، على سبيل المثال، دون قياس المنطقة التي سيمر من خلالها. باستخدام هذه النظرية فمن السهل القيام به الحسابات اللازمةلتحديد طول جزيرة تقع في وسط النهر دون السباحة إليها. إما تقوية السور بوضع القضيب في الامتداد بحيث يقسمه إلى مثلثين متساويين، أو حساب عناصر العمل المعقدة في النجارة، أو عند الحساب نظام الجمالونالأسطح أثناء البناء.

أول علامة على مساواة المثلثات لديها تطبيق واسعفي حياة "الكبار" الحقيقية. على الرغم من أن هذا الموضوع بالذات يبدو مملاً وغير ضروري على الإطلاق بالنسبة للكثيرين خلال سنوات الدراسة.