Was ist 1 Zeichen dafür, dass Dreiecke gleich sind? Das erste Zeichen der Gleichheit der Dreiecke. Das zweite und dritte Gleichheitszeichen der Dreiecke. Verhältnis der Elemente in einem rechtwinkligen Dreieck

Dreieck . Spitzes, stumpfes und rechtwinkliges Dreieck.

Beine und Hypotenuse. Gleichschenkliges und gleichseitiges Dreieck.

Winkelsumme eines Dreiecks.

Außenwinkel eines Dreiecks. Zeichen der Gleichheit von Dreiecken.

Bemerkenswerte Linien und Punkte in einem Dreieck: Höhen, Mittelwerte,

Halbierende, Median e Senkrechte, Orthozentrum,

Schwerpunkt, Mittelpunkt eines umschriebenen Kreises, Mittelpunkt eines eingeschriebenen Kreises.

Satz des Pythagoras. Seitenverhältnis in einem beliebigen Dreieck.

Dreieck ist ein Polygon mit drei Seiten (oder drei Winkeln). Die Seiten eines Dreiecks werden oft durch kleine Buchstaben gekennzeichnet, die den Großbuchstaben entsprechen, die die gegenüberliegenden Eckpunkte darstellen.

Wenn alle drei Winkel spitz sind (Abb. 20), dann ist dies der Fall spitzes Dreieck . Wenn einer der Winkel stimmt(C, Abb.21), dann das rechtwinkliges Dreieck; Seitena, beinen rechten Winkel bildend heißen Beine; SeiteC, Gegenteil rechter Winkel, angerufen Hypotenuse. Wenn einer von stumpfe Winkel (B, Abb. 22), dann das stumpfes Dreieck.


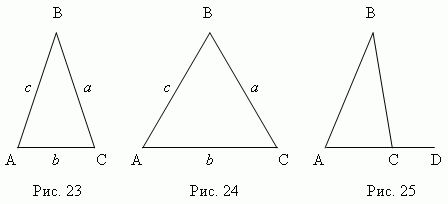
Dreieck ABC (Abb. 23) - gleichschenklig, Wenn zwei seine Seiten sind gleich (A= C); diese gleichen Seiten heißen seitlich, wird der Dritte aufgerufen Basis Dreieck. Dreieck ABC (Abb. 24) – gleichseitig, Wenn Alle seine Seiten sind gleich (A = B = C). Im allgemeinen Fall ( A ≠ B ≠ C) wir haben Skalen Dreieck .

Grundlegende Eigenschaften von Dreiecken. In jedem Dreieck:

1. Gegenüber der größeren Seite liegt der größere Winkel und umgekehrt.

2. Gleichen Winkeln liegen gleiche Seiten gegenüber und umgekehrt.

Insbesondere alle Winkel in gleichseitig Dreieck sind gleich.

3. Die Winkelsumme eines Dreiecks beträgt 180° º .

Aus den letzten beiden Eigenschaften folgt, dass jeder Winkel gleichseitig ist

Dreieck ist 60 º.

4. Fortsetzung einer der Seiten des Dreiecks (AC, Abb. 25), wir bekommen extern

Winkel BCD . Der Außenwinkel eines Dreiecks ist gleich der Summe der Innenwinkel,

nicht daneben : BCD = A + B.

5. Beliebig Die Seite eines Dreiecks ist kleiner als die Summe der beiden anderen Seiten und größer

ihre Unterschiede (A < B + C, A > B – C;B < A + C, B > A – C;C < A + B,C > A – B).

Zeichen der Gleichheit von Dreiecken.

Dreiecke sind kongruent, wenn sie jeweils gleich sind:

A ) zwei Seiten und der Winkel zwischen ihnen;

B ) zwei Ecken und die angrenzende Seite;

c) drei Seiten.

Zeichen der Gleichheit rechtwinkliger Dreiecke.

Zwei rechteckig Dreiecke sind gleich, wenn eine der folgenden Bedingungen erfüllt ist:

1) ihre Beine sind gleich;

2) der Schenkel und die Hypotenuse eines Dreiecks sind gleich dem Schenkel und der Hypotenuse des anderen;

3) die Hypotenuse und der spitze Winkel eines Dreiecks sind gleich der Hypotenuse und dem spitzen Winkel des anderen;

4) der Schenkel und der angrenzende spitze Winkel eines Dreiecks sind gleich dem Schenkel und der angrenzende spitze Winkel des anderen;

5) Das Bein und der entgegengesetzte spitze Winkel eines Dreiecks sind gleich dem Bein und der entgegengesetzte spitze Winkel des anderen.

Wundervolle Linien und Punkte im Dreieck.

Höhe Dreieck istsenkrecht,von jedem Scheitelpunkt auf die gegenüberliegende Seite abgesenkt werden ( oder seine Fortsetzung). Diese Seite heißtBasis des Dreiecks . Die drei Höhen eines Dreiecks schneiden sich immeran einem Punkt, angerufen Orthozentrum Dreieck. Orthozentrum eines spitzen Dreiecks (Punkt O , Abb. 26) liegt innerhalb des Dreiecks, undOrthozentrum eines stumpfen Dreiecks (Punkt O , Abb.27) – draußen; Das Orthozentrum eines rechtwinkligen Dreiecks fällt mit dem Scheitelpunkt des rechten Winkels zusammen.

Mittlere - Das Segment , die einen beliebigen Scheitelpunkt eines Dreiecks mit der Mitte der gegenüberliegenden Seite verbindet. Drei Mittellinien eines Dreiecks (AD, BE, CF, Abb.28) sich in einem Punkt schneiden O , immer innerhalb des Dreiecks liegend und sein sein Schwerpunkt. Dieser Punkt teilt jeden Median im Verhältnis 2:1, gezählt vom Scheitelpunkt.

Halbierende - Das Winkelhalbierendes Segment Winkel vom Scheitelpunkt zum Punkt Kreuzungen mit der gegenüberliegenden Seite. Drei Winkelhalbierende eines Dreiecks (AD, BE, CF, Abb. 29) sich in einem Punkt schneiden Oh, immer im Dreieck liegend Und Sein Mittelpunkt des eingeschriebenen Kreises(siehe Abschnitt „Beschriftetund umschriebene Polygone").

Die Winkelhalbierende teilt die gegenüberliegende Seite in Teile, die proportional zu den angrenzenden Seiten sind ; zum Beispiel in Abb. 29 AE: CE = AB: BC.

Mittelsenkrechte ist eine Senkrechte, die von der Mitte aus gezogen wird Segmentpunkte (Seiten). Drei Mittelsenkrechte des Dreiecks ABC(KO, MO, NEIN, Abb. 30 ) schneiden sich in einem Punkt O, nämlich Center umschriebener Kreis (Punkte K, M, N – die Mittelpunkte der Seiten des Dreiecks ABC).

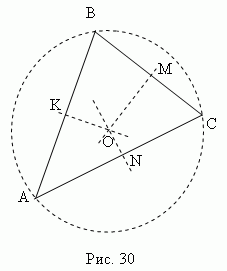
In einem spitzen Dreieck liegt dieser Punkt innerhalb des Dreiecks; im stumpfen - draußen; in einem Rechteck - in der Mitte der Hypotenuse. Orthozentrum, Schwerpunkt, Umkreismittelpunkt und Inkreis fallen nur in einem gleichseitigen Dreieck zusammen.

Satz des Pythagoras. In einem rechtwinkligen Dreieck das Quadrat der LängeDie Hypotenuse ist gleich der Summe der Quadrate der Beinlängen.

Der Beweis des Satzes des Pythagoras geht eindeutig aus Abb. 31 hervor. Betrachten Sie ein rechtwinkliges Dreieck ABC mit Beinen a, b und Hypotenuse C.

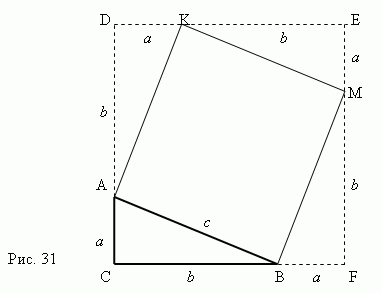
Lasst uns ein Quadrat bauen AKMB unter Verwendung der Hypotenuse AB als Seite. DannSetzen Sie die Seiten des rechtwinkligen Dreiecks fort ABC um ein Quadrat zu bekommen CDEF , dessen Seite gleich ista + b .Jetzt ist klar, dass die Fläche des Quadrats CDEF ist gleich ( a+b) 2 . Andererseits dies Fläche entspricht der Summe Bereiche vier rechtwinklige Dreiecke und das Quadrat AKMB, das heißt

C 2 + 4 (ab / 2) = C 2 + 2 ab,

von hier,

C 2 + 2 ab= (a+b) 2 ,

und schließlich haben wir:

C 2 =A 2 +b 2 .

Seitenverhältnis in einem beliebigen Dreieck.

Im allgemeinen Fall (für ein beliebiges Dreieck) gilt:

C 2 =A 2 +b 2 – 2ab· cos C,

wo C – Winkel zwischen den SeitenA Und B .

Zwei Dreiecke heißen kongruent, wenn sie durch Überlappung zusammengebracht werden können. Abbildung 1 zeigt gleiche Dreiecke ABC und A 1 B 1 C 1. Jedes dieser Dreiecke kann übereinander gelegt werden, sodass sie vollständig kompatibel sind, d. h. ihre Eckpunkte und Seiten sind paarweise kompatibel. Es ist klar, dass die Winkel dieser Dreiecke auch paarweise übereinstimmen werden.

Wenn also zwei Dreiecke kongruent sind, dann sind die Elemente (d. h. Seiten und Winkel) eines Dreiecks jeweils gleich den Elementen des anderen Dreiecks. Beachten Sie, dass in gleichen Dreiecken gegen entsprechend gleiche Seiten(d. h. Überlappung bei Überlagerung) gleiche Winkel liegen und zurück: Dabei liegen sich gleiche Seiten bzw. gleiche Winkel gegenüber.

So liegen beispielsweise in den in Abbildung 1 gezeigten gleichen Dreiecken ABC und A 1 B 1 C 1 gegenüberliegende gleiche Seiten AB und A 1 B 1 jeweils gleiche Winkel C und C 1. Wir bezeichnen die Gleichheit der Dreiecke ABC und A 1 B 1 C 1 wie folgt: Δ ABC = Δ A 1 B 1 C 1. Es stellt sich heraus, dass die Gleichheit zweier Dreiecke durch den Vergleich einiger ihrer Elemente festgestellt werden kann.

Satz 1. Das erste Zeichen der Gleichheit der Dreiecke. Wenn zwei Seiten und der Winkel zwischen ihnen eines Dreiecks jeweils gleich zwei Seiten und der Winkel zwischen ihnen eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent (Abb. 2).

Nachweisen. Betrachten Sie die Dreiecke ABC und A 1 B 1 C 1, in denen AB = A 1 B 1, AC = A 1 C 1 ∠ A = ∠ A 1 (siehe Abb. 2). Beweisen wir, dass Δ ABC = Δ A 1 B 1 C 1 .

Da ∠ A = ∠ A 1, kann das Dreieck ABC dem Dreieck A 1 B 1 C 1 so überlagert werden, dass der Scheitelpunkt A mit dem Scheitelpunkt A 1 ausgerichtet ist und die Seiten AB und AC jeweils den Strahlen A 1 B 1 und A 1 überlagert werden C 1. Da AB = A 1 B 1, AC = A 1 C 1, dann wird Seite AB mit Seite A 1 B 1 und Seite AC mit Seite A 1 C 1 ausgerichtet; insbesondere fallen die Punkte B und B 1, C und C 1 zusammen. Folglich werden die Seiten BC und B 1 C 1 ausgerichtet. Die Dreiecke ABC und A 1 B 1 C 1 sind also vollständig kompatibel, das heißt, sie sind gleich.

Satz 2 wird auf ähnliche Weise mit der Superpositionsmethode bewiesen.

Satz 2. Das zweite Zeichen der Gleichheit der Dreiecke. Wenn eine Seite und zwei benachbarte Winkel eines Dreiecks jeweils gleich der Seite und zwei benachbarte Winkel eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent (Abb. 34).

Kommentar. Basierend auf Satz 2 wird Satz 3 aufgestellt.

Satz 3. Die Summe zweier beliebiger Innenwinkel eines Dreiecks beträgt weniger als 180°.

Satz 4 folgt aus dem letzten Satz.

Satz 4. Ein Außenwinkel eines Dreiecks ist größer als jeder Innenwinkel, der nicht daran angrenzt.

Satz 5. Das dritte Zeichen der Gleichheit der Dreiecke. Wenn drei Seiten eines Dreiecks jeweils gleich drei Seiten eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent ().

Beispiel 1. In den Dreiecken ABC und DEF (Abb. 4)

∠ A = ∠ E, AB = 20 cm, AC = 18 cm, DE = 18 cm, EF = 20 cm. Vergleichen Sie die Dreiecke ABC und DEF. Welcher Winkel im Dreieck DEF ist gleich Winkel B?

Lösung. Diese Dreiecke sind nach dem ersten Vorzeichen gleich. Der Winkel F des Dreiecks DEF ist gleich dem Winkel B des Dreiecks ABC, da diese Winkel jeweils gegenüber den gleichen Seiten DE und AC liegen.

Beispiel 2. Die Segmente AB und CD (Abb. 5) schneiden sich im Punkt O, der jeweils in der Mitte liegt. Wie lang ist das Segment BD, wenn das Segment AC 6 m beträgt?

Lösung. Die Dreiecke AOC und BSB sind gleich (gemäß dem ersten Kriterium): ∠ AOC = ∠ BSB (vertikal), AO = OB, CO = OD (nach Bedingung).
Aus der Gleichheit dieser Dreiecke folgt, dass ihre Seiten gleich sind, d.h. AC = BD. Da aber gemäß der Bedingung AC = 6 m ist, dann ist BD = 6 m.

In dieser Lektion werden wir das erste Gleichheitszeichen von Dreiecken untersuchen. Zunächst formulieren und beweisen wir den Satz über das erste Kriterium für die Gleichheit von Dreiecken. Als nächstes werden wir Probleme mithilfe des ersten Gleichheitszeichens von Dreiecken lösen.

In der vorherigen Lektion haben wir das Konzept der „gleichen Dreiecke“ eingeführt – Dreiecke, die durch Überlappung kombiniert werden können. Allerdings ist es per Definition sehr schwierig, Zahlen zu vergleichen, daher werden wir Kriterien für die Gleichheit von Dreiecken einführen – nach einigen Elementen.

Reis. 1. Die Dreiecke ABC und A 1 B 1 C 1 sind gleich

Beweisen wir den Satz: Wenn zwei Seiten und der Winkel zwischen ihnen eines Dreiecks und die entsprechenden beiden Seiten und der Winkel zwischen ihnen des zweiten Dreiecks gleich sind, dann sind diese Dreiecke kongruent.

Satz: Gegeben. Beweisen Sie: ABC und .

Beweis: Lassen Sie uns die Daten in der Formbedingung überlagern. Als Ergebnis dieser Aktion fallen die Eckpunkte A und A 1, die Segmente AB und A 1 B 1, AC und A 1 C 1 zusammen. Wenn wir die Dreiecke als Ganzes betrachten, wird es mit zusammenfallen.

Der Satz ist bewiesen.

Betrachten wir mehrere Probleme.

Die Segmente AC und BD werden durch ihren Schnittpunkt O in zwei Hälften geteilt. Beweisen Sie das.

Beweis: Lassen Sie uns eine erklärende Zeichnung erstellen.

Reis. 2. Zeichnen zum Beispiel 1

Beachten Sie, dass die Winkel AOB und COD wie die vertikalen gleich sind und die Seiten BO und AO des Dreiecks AOB jeweils gleich den Seiten OD und OC des Dreiecks COD sind. Daher sind die Dreiecke AOB und COD nach dem ersten Kriterium gleich.

Die Segmente AC und BD werden durch den Schnittpunkt in zwei Hälften geteilt. Beweisen Sie das.

Reis. 3. Zeichnen zum Beispiel 2

In der vorherigen Aufgabe haben wir das anhand des ersten Zeichens bewiesen. Aus diesen Überlegungen können wir schließen, dass AB = CD, ∠OAB = ∠OCD.

Schauen wir uns nun die Dreiecke an . Sie haben AC – eine gemeinsame Seite, AB = CD und ∠CAB = ∠ACD (wie bewiesen). Daher nach dem ersten Zeichen der Gleichheit. Q.E.D.

Reis. 4. Zeichnen zum Beispiel 3

In Abbildung 3 sind die Segmente AB und AC gleich. Winkel 1 ist gleich Winkel 2. Es ist bekannt, dass AC = 15 cm, DC = 5 cm. Beweisen Sie, dass . Finden Sie die Längen der Segmente BD und AB.

Die Dreiecke sind nach dem ersten Kriterium gleich, weil ∠1 = ∠2, AB = AC und AD die gemeinsame Seite beider Dreiecke ist. Aus der Gleichheit der Dreiecke folgt, dass einige ihrer entsprechenden Elemente gleich sind, also: BD = CD = 5 cm,

AB = AC = 15 cm.

Antwort: 5 cm, 15 cm.

In Abbildung 5 BC = AD. Winkel 1 ist gleich Winkel 2, AD = 17 cm, CD = 14 cm. Beweisen Sie, dass . Finden Sie AB und BC.

Reis. 5. Zeichnen zum Beispiel 4

Das Dreieck ABC ist gleich dem Dreieck CDA. nach dem ersten Zeichen. ∠1 = ∠2, CB = AD und AC ist die gemeinsame Seite beider Dreiecke. Daraus folgt, dass .

1. Unterrichtsthema „Das erste Zeichen der Dreiecksgleichheit“
2. Dreieck. Verzeichnis

1. Nr. 36. Butuzov V.F., Kadomtsev S.B., Prasolova V.V. Geometrie 7 / V.F. Butuzov, S.B. Kadomtsev, V.V. Prasolova, Hrsg. Sadovnichego V.A. - M.: Bildung, 2010.

2. Beweisen Sie, dass die Dreiecke BOA und EOC kongruent sind. Die Segmente BE und AC werden durch ihren Schnittpunkt in zwei Hälften geteilt.

3. Beweisen Sie, dass eine Gerade, die gleiche Segmente von den Seiten eines Winkels schneidet, senkrecht zu seiner Winkelhalbierenden steht.

4. *Auf den Seiten des Winkels M werden gleiche Segmente MA und MC aufgetragen und seine Winkelhalbierende gezeichnet, auf der Punkt B markiert ist. Beweisen Sie, dass BM die Winkelhalbierende des Winkels ABC ist.

Ticket 2

Frage 1

Tests für die Gleichheit von Dreiecken (Beweis für alles)

1. Zeichen Gleichheit der Dreiecke: auf zwei Seiten und der Winkel zwischen ihnen ( Satz 3.1. – Gleichheitszeichen von Dreiecken mit zwei Seiten und dem Winkel zwischen ihnen – Wenn zwei Seiten und der Winkel zwischen ihnen eines Dreiecks jeweils gleich zwei Seiten und dem Winkel zwischen ihnen eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent)

Nachweisen:

Lassen Sie die Dreiecke ABC und A 1 B 1 C 1 den Winkel A gleich A 1, AB gleich A 1 B 1 und AC gleich A 1 C 1 haben. Beweisen wir, dass die Dreiecke gleich sind.

Da A 1 B 1 gleich A 1 B 2 ist, fällt der Scheitelpunkt B 2 mit B 1 zusammen. Da der Winkel B 1 A 1 C 1 gleich dem Winkel B 2 A 1 C 2 ist, dann ist der Strahl A 1 C 2 wird mit A 1 C 1 zusammenfallen. Da A 1 C 1 gleich A 1 C 2 ist, fällt C 2 mit C 1 zusammen. Dies bedeutet, dass das Dreieck A 1 B 1 C 1 mit dem Dreieck A 1 B 2 C 2 zusammenfällt, was bedeutet, dass es gleich ist das Dreieck ABC.

Der Satz ist bewiesen.

2 Zeichen Gleichheit der Dreiecke: entlang der Seite und benachbarter Winkel (Satz 3.2. - Gleichheitszeichen von Dreiecken nach Seite und angrenzenden Winkeln – Wenn eine Seite und ihre angrenzenden Winkel eines Dreiecks jeweils gleich der Seite und den angrenzenden Winkeln eines anderen Dreiecks sind, dann sind diese Dreiecke kongruent)

Nachweisen:

Lassen ABC und A 1 B 1 C 1 sind zwei Dreiecke, in denen AB gleich A 1 B 1 ist, Winkel A gleich Winkel A 1 ist und Winkel B gleich Winkel B 1 ist. Beweisen wir, dass sie gleich sind.

Sei A 1 B 2 C 2 ein Dreieck gleich ABC, mit Scheitelpunkt B 2 auf Strahl A 1 B 1 und Scheitelpunkt C 2 in derselben Halbebene relativ zur Geraden A 1 B 1, wo Scheitelpunkt C 1 liegt.

Da A 1 B 2 gleich A 1 B 1 ist, fällt der Scheitelpunkt von B 2 mit B 1 zusammen. Da der Winkel B 1 A 1 C 2 gleich dem Winkel B 1 A 1 C 1 und dem Winkel A1B1C2 ist gleich dem Winkel A1B1C1 ist, dann fällt Strahl A 1 C 2 mit A 1 C 1 zusammen und B 1 C 2 fällt mit B 1 C 1 zusammen. Daraus folgt, dass der Scheitelpunkt C 2 mit C 1 zusammenfällt. Dies bedeutet, dass das Dreieck A 1 B 1 C 1 mit dem Dreieck A 1 B 2 C 2 zusammenfällt, was bedeutet, dass es gleich dem Dreieck ABC ist.

Der Satz ist bewiesen.

3 Zeichen Gleichheit der Dreiecke: auf drei Seiten (Satz 3.6. - Test auf Gleichheit von Dreiecken auf drei Seiten – Wenn drei Seiten eines Dreiecks jeweils gleich den drei Seiten eines anderen Dreiecks sind, dann sind diese Dreiecke kongruent)

Nachweisen:

Lassen ABC und A 1 B 1 C 1 sind zwei Dreiecke, in denen AB gleich A 1 B 1, AC gleich A 1 C 1 und BC gleich B 1 C 1 ist. Beweisen wir, dass sie gleich sind.

Nehmen wir an, die Dreiecke sind nicht gleich. Dann ist ihr Winkel A nicht gleich Winkel A 1, Winkel B ist nicht gleich Winkel B 1 und Winkel C ist nicht gleich Winkel C 1. Ansonsten wären sie, gemessen an den Federn, gleich.

Sei A 1 B 1 C 2 ein Dreieck gleich dem Dreieck ABC, dessen Scheitelpunkt C 2 in derselben Halbebene wie Scheitelpunkt C 1 relativ zur Linie A 1 B 1 liegt.

Sei D der Mittelpunkt des Segments C 1 C 2. Die Dreiecke A 1 C 1 C 2 und B 1 C 1 C 2 sind gleichschenklig mit einer gemeinsamen Basis C 1 C 2. Daher sind ihre Mediane A 1 D und B 1 D Höhen, was bedeutet, dass die Linien A 1 D und B 1 D senkrecht zur Linie C 1 C 2 stehen. Die Linien A 1 D und B 1 D fallen nicht zusammen, da die Punkte A 1, B 1 , D liegen nicht auf derselben Geraden, aber durch den Punkt D der Geraden C 1 C 2 kann nur eine Gerade senkrecht dazu gezogen werden. Wir sind zu einem Widerspruch gelangt.

Unter der großen Anzahl von Polygonen, die im Wesentlichen eine geschlossene, sich nicht schneidende gestrichelte Linie darstellen, ist das Dreieck die Figur mit den wenigsten Winkeln. Mit anderen Worten, dies ist das einfachste Polygon. Doch trotz aller Einfachheit birgt diese Figur viele Geheimnisse und interessante Entdeckungen, die durch einen besonderen Zweig der Mathematik – die Geometrie – beleuchtet werden. Ab der siebten Klasse wird diese Disziplin in Schulen unterrichtet, wobei dem Thema „Dreieck“ besondere Aufmerksamkeit geschenkt wird. Kinder lernen nicht nur die Regeln für die Figur selbst, sondern vergleichen sie auch, indem sie das 1., 2. und 3. Gleichheitszeichen von Dreiecken studieren.

Erste Bekanntschaft

Eine der ersten Regeln, die Schulkinder lernen, lautet etwa so: Die Summe der Werte aller Winkel eines Dreiecks beträgt 180 Grad. Um dies zu bestätigen, reicht es aus, jeden Eckpunkt mit einem Winkelmesser zu messen und alle resultierenden Werte zu addieren. Auf dieser Grundlage lässt sich aus zwei bekannten Größen leicht die dritte bestimmen. Zum Beispiel: In einem Dreieck beträgt einer der Winkel 70° und der andere 85°. Wie groß ist der dritte Winkel?

180 - 85 - 70 = 25.

Antwort: 25°.

Probleme können komplexer sein, wenn nur ein Winkelwert angegeben wird und der zweite Wert nur angibt, um wie viel oder um wie viel Mal er größer oder kleiner ist.

Um bestimmte Merkmale eines Dreiecks zu bestimmen, können spezielle Linien gezeichnet werden, von denen jede ihren eigenen Namen hat:

• Höhe – eine senkrechte gerade Linie, die vom Scheitelpunkt zur gegenüberliegenden Seite gezogen wird;
• alle drei gleichzeitig gezeichneten Höhen schneiden sich in der Mitte der Figur und bilden ein Orthozentrum, das je nach Dreieckstyp sowohl innen als auch außen liegen kann;
• Median – eine Linie, die den Scheitelpunkt mit der Mitte der gegenüberliegenden Seite verbindet;
• der Schnittpunkt der Mediane ist der Schwerpunkt, der sich innerhalb der Figur befindet;
• Winkelhalbierende – eine Linie, die vom Scheitelpunkt zum Schnittpunkt mit der gegenüberliegenden Seite verläuft; der Schnittpunkt von drei Winkelhalbierenden ist der Mittelpunkt des eingeschriebenen Kreises.

Einfache Wahrheiten über Dreiecke

Dreiecke haben, wie alle Formen, ihre eigenen Eigenschaften und Eigenschaften. Wie bereits erwähnt, handelt es sich bei dieser Figur um das einfachste Polygon, jedoch mit eigenen charakteristischen Merkmalen:

• der Winkel mit dem größeren Wert liegt immer gegenüber der längsten Seite und umgekehrt;
• Gleiche Winkel liegen gleichen Seiten gegenüber, ein Beispiel hierfür ist ein gleichschenkliges Dreieck;
• die Summe der Innenwinkel ist immer gleich 180°, was bereits an einem Beispiel gezeigt wurde;
• Wenn eine Seite des Dreiecks über seine Grenzen hinaus ausgedehnt wird, entsteht es Außenecke, die immer gleich der Summe der nicht benachbarten Winkel ist;
• Jede Seite ist immer kleiner als die Summe der beiden anderen Seiten, aber größer als deren Differenz.

Arten von Dreiecken

Der nächste Schritt der Bekanntschaft besteht darin, die Gruppe zu bestimmen, zu der das präsentierte Dreieck gehört. Die Zugehörigkeit zu dem einen oder anderen Typ hängt von der Größe der Winkel des Dreiecks ab.

• Gleichschenklig – mit zwei gleichen Seiten, die seitlich genannt werden, wobei die dritte in diesem Fall als Basis der Figur dient. Die Winkel an der Basis eines solchen Dreiecks sind gleich, und der vom Scheitelpunkt ausgehende Median ist die Winkelhalbierende und die Höhe.
• Ein regelmäßiges oder gleichseitiges Dreieck ist ein Dreieck, bei dem alle Seiten gleich sind.
• Rechteckig: Einer seiner Winkel beträgt 90°. In diesem Fall wird die diesem Winkel gegenüberliegende Seite Hypotenuse und die anderen beiden Schenkel genannt.
• Spitzes Dreieck – alle Winkel betragen weniger als 90°.
• Stumpf – einer der Winkel größer als 90°.

Gleichheit und Ähnlichkeit von Dreiecken

Während des Lernprozesses betrachten sie nicht nur eine einzelne Figur, sondern vergleichen auch zwei Dreiecke. Und dieses scheinbar einfache Thema enthält viele Regeln und Theoreme, mit denen bewiesen werden kann, dass es sich bei den betreffenden Figuren um gleiche Dreiecke handelt. Die Kriterien für die Gleichheit von Dreiecken haben folgende Definition: Dreiecke sind gleich, wenn ihre entsprechenden Seiten und Winkel gleich sind. Wenn Sie bei dieser Gleichheit diese beiden Figuren übereinander legen, konvergieren alle ihre Linien. Auch können die Figuren ähnlich sein, insbesondere gilt dies für nahezu identische Figuren, die sich nur in der Größe unterscheiden. Um eine solche Schlussfolgerung über die dargestellten Dreiecke ziehen zu können, muss eine der folgenden Bedingungen erfüllt sein:

• zwei Winkel einer Figur sind gleich zwei Winkeln einer anderen;
• Die beiden Seiten des einen sind proportional zu den beiden Seiten des zweiten Dreiecks, und die von den Seiten gebildeten Winkel sind gleich.
• Drei Seiten der zweiten Figur sind die gleichen wie die erste.

Für eine unbestreitbare Gleichheit, die nicht den geringsten Zweifel aufkommen lässt, ist es natürlich notwendig, die gleichen Werte aller Elemente beider Figuren zu haben, jedoch wird die Aufgabe durch die Verwendung von Theoremen stark vereinfacht und nur wenige Bedingungen dürfen die Gleichheit von Dreiecken beweisen.

Das erste Zeichen der Gleichheit der Dreiecke

Probleme zu diesem Thema werden auf der Grundlage des Beweises des Satzes gelöst, der so lautet: „Wenn zwei Seiten eines Dreiecks und der Winkel, den sie bilden, gleich zwei Seiten und dem Winkel eines anderen Dreiecks sind, dann sind auch die Figuren gleich.“ gegenseitig."

Wie klingt der Beweis des Satzes über das erste Gleichheitszeichen von Dreiecken? Jeder weiß, dass zwei Segmente gleich sind, wenn sie die gleiche Länge haben, oder Kreise gleich sind, wenn sie den gleichen Radius haben. Und im Fall von Dreiecken gibt es mehrere Zeichen, bei denen wir davon ausgehen können, dass die Figuren identisch sind, was bei der Lösung verschiedener geometrischer Probleme sehr praktisch ist.

Wie der Satz „Das erste Zeichen der Gleichheit von Dreiecken“ klingt, wurde oben beschrieben, aber hier ist sein Beweis:

• Angenommen, die Dreiecke ABC und A 1 B 1 C 1 haben die gleichen Seiten AB und A 1 B 1 und dementsprechend BC und B 1 C 1, und die von diesen Seiten gebildeten Winkel sind gleich groß, das heißt, sie sind gleich. Dann erhalten wir durch Überlagerung von △ ABC mit △ A 1 B 1 C 1 die Übereinstimmung aller Geraden und Eckpunkte. Daraus folgt, dass diese Dreiecke absolut identisch und daher einander gleich sind.

Der Satz „Das erste Zeichen der Gleichheit von Dreiecken“ wird auch „Auf zwei Seiten und einem Winkel“ genannt. Eigentlich ist das sein Wesen.

Satz über das zweite Zeichen

Das zweite Gleichheitszeichen wird auf ähnliche Weise bewiesen; der Beweis basiert auf der Tatsache, dass die Figuren bei der Überlagerung an allen Ecken und Seiten vollständig übereinstimmen. Und der Satz klingt so: „Wenn eine Seite und zwei Winkel, an deren Bildung es beteiligt ist, der Seite und zwei Winkeln des zweiten Dreiecks entsprechen, dann sind diese Figuren identisch, also gleich.“

Drittes Zeichen und Beweis

Wenn sowohl das 2. als auch das 1. Gleichheitszeichen der Dreiecke sowohl die Seiten als auch die Ecken der Figur betrafen, dann bezieht sich das 3. nur auf die Seiten. Der Satz hat also die folgende Formulierung: „Wenn alle Seiten eines Dreiecks gleich drei Seiten des zweiten Dreiecks sind, dann sind die Figuren identisch.“

Um diesen Satz zu beweisen, müssen wir uns genauer mit der Definition von Gleichheit befassen. Was bedeutet im Wesentlichen der Ausdruck „Dreiecke sind gleich“? Identität besagt, dass, wenn man eine Figur über eine andere legt, alle ihre Elemente übereinstimmen. Dies kann nur dann der Fall sein, wenn ihre Seiten und Winkel gleich sind. Gleichzeitig ist der Winkel gegenüber einer der Seiten, der derselbe ist wie der des anderen Dreiecks, gleich dem entsprechenden Scheitelpunkt der zweiten Figur. Es ist zu beachten, dass der Beweis an dieser Stelle leicht auf ein Kriterium für die Gleichheit von Dreiecken übertragen werden kann. Wenn eine solche Reihenfolge nicht eingehalten wird, ist die Gleichheit der Dreiecke einfach unmöglich, außer in Fällen, in denen die Figur ein Spiegelbild der ersten ist.

Rechtwinklige Dreiecke

Die Struktur solcher Dreiecke hat immer Eckpunkte mit einem Winkel von 90°. Daher sind die folgenden Aussagen wahr:

• Dreiecke mit rechten Winkeln sind gleich, wenn die Schenkel des einen mit den Schenkeln des zweiten identisch sind;
• Figuren sind gleich, wenn ihre Hypotenusen und eines ihrer Beine gleich sind;
• Solche Dreiecke sind kongruent, wenn ihre Schenkel und ihr spitzer Winkel identisch sind.

Dieses Zeichen bezieht sich auf Um den Satz zu beweisen, wenden sie die Anwendung von Figuren aufeinander an, wodurch die Dreiecke an den Beinen gefaltet werden, sodass zwei Geraden mit den Seiten CA und CA 1 entstehen.

Praktische Anwendung

In den meisten Fällen wird in der Praxis das erste Gleichheitszeichen von Dreiecken verwendet. Tatsächlich wird ein so scheinbar einfaches Thema der 7. Klasse zu Geometrie und Planimetrie auch verwendet, um beispielsweise die Länge eines Telefonkabels zu berechnen, ohne die Fläche zu messen, durch die es verläuft. Mit diesem Satz lässt sich das ganz einfach bewerkstelligen notwendigen Berechnungen um die Länge einer Insel zu bestimmen, die mitten in einem Fluss liegt, ohne dorthin zu schwimmen. Verstärken Sie entweder den Zaun, indem Sie das Brett so in die Spannweite legen, dass es ihn in zwei gleiche Dreiecke teilt, oder berechnen Sie komplexe Arbeitselemente im Tischlerhandwerk oder beim Berechnen Sparrensystem Dächer während der Bauphase.

Das erste Zeichen der Gleichheit von Dreiecken ist breite Anwendung im wirklichen „Erwachsenenleben“. Obwohl dieses spezielle Thema während der Schulzeit für viele langweilig und völlig unnötig erscheint.