In jedem akademischen Studiengang beginnt das Studium der Physik mit der Mechanik. Nicht mit theoretischer, nicht mit angewandter und nicht rechnerischer, sondern mit der guten alten klassischen Mechanik. Diese Mechanik wird auch Newtonsche Mechanik genannt. Der Legende nach ging der Wissenschaftler im Garten spazieren, sah einen Apfel fallen, und es war dieses Phänomen, das ihn zur Entdeckung des universellen Gravitationsgesetzes trieb. Natürlich hat es das Gesetz schon immer gegeben, und Newton hat ihm nur eine Form gegeben, die die Leute verstehen, aber sein Verdienst ist unbezahlbar. In diesem Artikel werden wir die Gesetze der Newtonschen Mechanik nicht so detailliert wie möglich beschreiben, sondern die Grundlagen, Grundkenntnisse, Definitionen und Formeln skizzieren, die Ihnen immer in die Hände spielen können.
Die Mechanik ist ein Teilgebiet der Physik, eine Wissenschaft, die die Bewegung materieller Körper und die Wechselwirkungen zwischen ihnen untersucht.
Das Wort selbst ist griechischen Ursprungs und wird mit „die Kunst des Maschinenbaus“ übersetzt. Aber vor dem Bau von Maschinen sind wir immer noch wie der Mond, also werden wir in die Fußstapfen unserer Vorfahren treten und die Bewegung von schräg zum Horizont geworfenen Steinen und aus einer Höhe von . auf den Kopf fallenden Äpfeln studieren h.

Warum beginnt das Physikstudium mit der Mechanik? Weil es ganz natürlich ist, es nicht vom thermodynamischen Gleichgewicht aus zu starten?!
Die Mechanik ist eine der ältesten Wissenschaften, und historisch gesehen begann das Studium der Physik genau mit den Grundlagen der Mechanik. Im Rahmen von Zeit und Raum platziert, konnten die Menschen mit all ihren Wünschen tatsächlich nicht von etwas anderem ausgehen. Bewegte Körper sind das Erste, worauf wir unsere Aufmerksamkeit richten.
Was ist Bewegung?
Mechanische Bewegung ist eine zeitliche Veränderung der Position von Körpern im Raum zueinander.
Nach dieser Definition kommen wir ganz natürlich zum Begriff des Bezugsrahmens. Ändern der Position von Körpern im Raum relativ zueinander. Stichworte Hier: relativ zueinander ... Schließlich bewegt sich ein Beifahrer in einem Auto relativ zu einer am Straßenrand stehenden Person mit einer bestimmten Geschwindigkeit und ruht relativ zu seinem Nachbarn auf dem Sitz neben ihm und bewegt sich mit einer anderen Geschwindigkeit relativ zu einem Beifahrer in einem Auto, das sie überholt.

Um normalerweise die Parameter von sich bewegenden Objekten zu messen und nicht verwirrt zu werden, brauchen wir Bezugsrahmen - starr miteinander verbundener Bezugskörper, Koordinatensystem und Uhr. Zum Beispiel bewegt sich die Erde in einem heliozentrischen Bezugssystem um die Sonne. Im Alltag führen wir fast alle unsere Messungen in einem geozentrischen Bezugssystem der Erde durch. Die Erde ist ein Bezugskörper, zu dem sich Autos, Flugzeuge, Menschen, Tiere bewegen.

Die Mechanik als Wissenschaft hat ihre eigene Aufgabe. Die Aufgabe der Mechanik besteht darin, jederzeit die Position eines Körpers im Raum zu kennen. Mit anderen Worten, die Mechanik konstruiert eine mathematische Beschreibung der Bewegung und findet Verbindungen zwischen physikalische Quantitäten charakterisieren es.
Um weiterzukommen, brauchen wir das Konzept „ materieller Punkt “. Sie sagen Physik - exakte Wissenschaft, aber Physiker wissen, wie viele Näherungen und Annahmen gemacht werden müssen, um genau diese Genauigkeit zu erreichen. Niemand hat jemals einen materiellen Punkt gesehen oder ideales Gas gerochen, aber sie sind es! Es ist einfach viel einfacher, mit ihnen zu leben.
Materieller Punkt ist ein Körper, dessen Größe und Form im Rahmen dieser Problemstellung vernachlässigt werden kann.
Abschnitte der klassischen Mechanik
Mechanik besteht aus mehreren Abschnitten
- Kinematik
- Dynamik
- Statik
Kinematik Aus physikalischer Sicht untersucht es genau, wie sich der Körper bewegt. Mit anderen Worten, dieser Abschnitt befasst sich mit den quantitativen Merkmalen der Bewegung. Geschwindigkeit, Weg finden - typische kinematische Probleme
Dynamik löst die Frage, warum es sich so bewegt. Das heißt, es berücksichtigt die auf den Körper einwirkenden Kräfte.
Statik untersucht das Gleichgewicht von Körpern unter Einwirkung von Kräften, beantwortet also die Frage: Warum fällt es überhaupt nicht?
Die Grenzen der Anwendbarkeit der klassischen Mechanik
Die klassische Mechanik hat nicht mehr den Anspruch, eine alles erklärende Wissenschaft zu sein (zu Beginn des letzten Jahrhunderts war alles noch ganz anders) und hat einen klaren Anwendungsrahmen. Generell gelten die Gesetze der klassischen Mechanik für die uns von der Größe her gewohnte Welt (Makrokosmos). Sie hören im Fall der Teilchenwelt auf zu funktionieren, wenn die Quantenmechanik die klassische ersetzt. Auch ist die klassische Mechanik nicht anwendbar auf Fälle, in denen die Bewegung von Körpern mit einer Geschwindigkeit nahe der Lichtgeschwindigkeit erfolgt. In solchen Fällen werden relativistische Effekte ausgeprägt. Grob gesagt ist dies im Rahmen der Quanten- und relativistischen Mechanik - der klassischen Mechanik - ein Sonderfall, wenn die Abmessungen des Körpers groß und die Geschwindigkeit klein ist.

Im Allgemeinen gehen Quanten- und relativistische Effekte nirgendwo hin, sie treten auch während der gewöhnlichen Bewegung makroskopischer Körper mit einer viel geringeren Geschwindigkeit als Lichtgeschwindigkeit auf. Eine andere Sache ist, dass der Effekt dieser Effekte so gering ist, dass er nicht über die genauesten Messungen hinausgeht. Somit wird die klassische Mechanik nie ihre grundlegende Bedeutung verlieren.
Wir werden uns in zukünftigen Artikeln weiterhin mit den physikalischen Grundlagen der Mechanik beschäftigen. Für ein besseres Verständnis der Mechanik können Sie jederzeit auf an unsere Autoren welches in individuell wird den dunklen Fleck der schwierigsten Aufgabe erhellen.
staatliche autonome Einrichtung
Kaliningrader Gebiet
professionelle Bildungsorganisation
Hochschule für Service und Tourismus
Vorlesungsreihe mit Praxisbeispielen
"Grundlagen der Theoretischen Mechanik"
nach DisziplinTechnische Mechanik
für Studierende3 Kurs
Spezialität20.02.04 Brandschutz
Kaliningrad
GENEHMIGT
Stellvertretender Direktor für UR GAU KO VET KSTN. Myasnikova
GENEHMIGT
Methodischer Rat der GAU KO POO KST
BERÜCKSICHTIGT
Bei einer Sitzung des PCC
Redaktion:
Kolganova A.A., Methodikerin
Falaleeva A.B., Lehrerin für russische Sprache und Literatur
Tsvetaeva L.V., Vorsitzende des PCCallgemeine mathematische und naturwissenschaftliche Disziplinen
Zusammengestellt von:
I. V. Nezvanova Lehrer von GAU KO VET KST
Inhalt
Theoretische Informationen
Theoretische Informationen
Beispiele zur Lösung praktischer Probleme
Dynamik: Grundbegriffe und Axiome
Theoretische Informationen
Beispiele zur Lösung praktischer Probleme
Referenzliste
Theoretische Informationen
Statik: Grundbegriffe und Axiome.
Statik - ein Abschnitt der theoretischen Mechanik, der die Eigenschaften von Kräften betrachtet, die auf die Punkte eines starren Körpers ausgeübt werden, und die Bedingungen für deren Gleichgewicht. Hauptaufgaben:
1. Transformationen von Kräftesystemen in äquivalente Kräftesysteme.
2. Bestimmung von Gleichgewichtsbedingungen für Kräftesysteme, die auf einen starren Körper wirken.
Materialpunkt nennt man das einfachste Modell eines materiellen Körpers
jede Form, deren Abmessungen klein genug sind und die als geometrischer Punkt mit einer bestimmten Masse angesehen werden kann. Jede Menge materieller Punkte wird als mechanisches System bezeichnet. Ein absolut fester Körper ist ein mechanisches System, dessen Abstände zwischen den Punkten sich bei keiner Wechselwirkungen ändern.
Leistung Ist ein Maß für die mechanische Wechselwirkung von materiellen Körpern untereinander. Kraft ist eine Vektorgröße, da sie durch drei Elemente bestimmt wird:
numerischer Wert;
Richtung;
Anwendungspunkt (A).
Die Maßeinheit für Kraft ist Newton (N).

Abbildung 1.1
Ein Kräftesystem ist eine Kombination von Kräften, die auf einen Körper einwirken.
Ein ausgeglichenes (gleich Null) System von Kräften wird ein System genannt, das, wenn es auf einen Körper angewendet wird, seinen Zustand nicht ändert.
Das auf den Körper einwirkende Kräftesystem kann durch ein resultierendes, als Kräftesystem wirkendes System ersetzt werden.
Axiome der Statik.
Axiom 1: Wird auf den Körper ein ausgewogenes Kräftesystem ausgeübt, so bewegt er sich gleichmäßig und geradlinig oder ruht (Trägheitsgesetz).
Axiom 2:
Ein absolut starrer Körper befindet sich unter der Wirkung zweier Kräfte genau dann im Gleichgewicht, wenn diese Kräfte gleich groß sind, in einer Geraden wirken und in entgegengesetzte Richtungen gerichtet sind. Abbildung 1.2
Axiom 3:
Der mechanische Zustand des Körpers wird nicht gestört, wenn ein ausgeglichenes Kräftesystem zu dem auf ihn wirkenden Kräftesystem hinzugefügt oder davon abgezogen wird.
Axiom 4: Die Resultierende zweier auf den Körper einwirkender Kräfte ist gleich ihrer geometrischen Summe, d. h. sie wird in Betrag und Richtung durch die Diagonale des auf diesen Kräften aufgebauten Parallelogramms wie auf den Seiten ausgedrückt.
Abbildung 1.3.
Axiom 5:
Die Kräfte, mit denen zwei Körper aufeinander einwirken, sind immer gleich groß und entlang einer Geraden in entgegengesetzte Richtungen gerichtet.
Abbildung 1.4.
Bindungsarten und ihre Reaktionen
Links
alle Beschränkungen, die die Bewegung eines Körpers im Raum verhindern, werden genannt. Der Körper, der unter der Wirkung der aufgebrachten Kräfte bemüht ist, die durch die Verbindung behinderte Bewegung auszuführen, wird auf ihn mit einer Kraft einwirken, genannt Druck auf die Kommunikation
... Nach dem Gesetz der Gleichheit von Wirkung und Reaktion wirkt die Verbindung mit dem gleichen Modul, aber entgegengesetzt gerichteter Kraft auf den Körper.
Die Kraft, mit der diese Verbindung wirkt auf den Körper, verhindert die eine oder andere Bewegung, heißt die Stärke der Reaktion (Reaktion) der Verbindung
.
Eine der wichtigsten Bestimmungen der Mechanik ist Bond-Release-Prinzip
:
jeder unfreie Körper kann als frei angesehen werden, wenn man Verbindungen verwirft und ihre Aktion durch Reaktionen von Verbindungen ersetzt.
Die Reaktion der Verbindung ist in die entgegengesetzte Richtung zu derjenigen gerichtet, in der die Verbindung keine Bewegung des Körpers zulässt. Die wichtigsten Bindungsarten und ihre Reaktionen sind in Tabelle 1.1 aufgeführt.
Tabelle 1.1
Bindungsarten und ihre Reaktionen
Kommunikationsname
Symbol
1
Glatte Oberfläche (Unterstützung)
- Oberfläche (Auflage), Reibung, auf der der gegebene Körper vernachlässigt werden kann.
Mit kostenloser Unterstützung, die Reaktionsenkrecht zur durch den Punkt gezogenen Tangente geführtEIN
Körperkontakt1
mit Auflagefläche2
.

2
Gewinde (flexibel, nicht dehnbar). Die in Form eines nicht dehnbaren Gewindes ausgeführte Verbindung verhindert, dass sich der Körper vom Aufhängepunkt wegbewegt. Daher ist die Reaktion des Fadens entlang des Fadens bis zum Punkt seiner Aufhängung gerichtet.

3
Schwerelose Rute
- eine Stange, deren Gewicht im Vergleich zur wahrgenommenen Belastung vernachlässigt werden kann.
Die Reaktion eines schwerelos aufklappbaren geradlinigen Stabes ist entlang der Stabachse gerichtet.

4
Bewegliches Scharnier, Scharnier-bewegliche Unterstützung. Die Reaktion ist entlang der Normalen zur Trägeroberfläche gerichtet.

7
Starre Beendigung.
In der Ebene der starren Termination gibt es zwei Komponenten der Reaktion,
und das Moment eines Kräftepaaresdie verhindert, dass sich der Balken dreht1
relativ zum PunktEIN
.
Die starre Fixierung im Raum nimmt dem Körper 1 alle sechs Freiheitsgrade weg - drei Verschiebungen entlang der Koordinatenachsen und drei Drehungen um diese Achsen.
In einem räumlich starren Abschluss gibt es drei Komponenten,
,
und drei Momente von Kräftepaaren![]() .
.

System konvergierender Kräfte
Ein System konvergierender Kräfte
heißt ein Kräftesystem, dessen Wirkungslinien sich in einem Punkt schneiden. Zwei in einem Punkt konvergierende Kräfte können nach dem dritten Axiom der Statik durch eine Kraft ersetzt werden -resultierende
.
Der Hauptvektor des Kräftesystems
- ein Wert gleich der geometrischen Summe der Kräfte des Systems.
Das resultierende ebene System konvergierender Kräfte kann bestimmt werdengrafisch und analytisch.
Ergänzung des Kräftesystems . Die Addition eines flachen Systems konvergierender Kräfte erfolgt entweder durch sukzessive Addition von Kräften unter Bildung einer Zwischenresultierenden (Abb. 1.5) oder durch Konstruktion eines Kraftpolygons (Abb. 1.6).


Abbildung 1.5 Abbildung 1.6
Achsenkraftprojektion
- eine algebraische Größe gleich dem Produkt des Kraftmoduls mit dem Kosinus des Winkels zwischen der Kraft und der positiven Richtung der Achse.
ProjektionFx(Bild 1.7) Achskräfte xpositiv, wenn der Winkel α spitz ist, negativ, wenn der Winkel α stumpf ist. Wenn die Stärkesenkrecht zur Achse steht, dann ist seine Projektion auf die Achse Null.

Abbildung 1.7
Projektion auf Ebene erzwingen Oh- Vektor , eingeschlossen zwischen den Projektionen von Anfang und Ende der Kraftauf diese Ebene. Jene. die Projektion der Kraft auf die Ebene ist eine Vektorgröße, die nicht nur durch einen Zahlenwert, sondern auch durch die Richtung in der Ebene gekennzeichnet istOh (Abbildung 1.8).

Abbildung 1.8
Dann das Projektionsmodul im Flugzeug Oh wird gleich sein:
Fxy = F cosα,
wobei α der Winkel zwischen der Kraftrichtung ist und seine Projektion.
Ein analytischer Weg, Kräfte zu setzen
.
Für eine analytische Art, Stärke zu setzenes ist notwendig, ein Koordinatensystem auszuwählenOhyz, in Bezug auf die die Kraftrichtung im Raum bestimmt wird.
Vektor, der Stärke darstellt, aufgetragen werden, wenn der Modul dieser Kraft und die Winkel α, β, γ, die die Kraft mit den Koordinatenachsen bildet, bekannt sind. PunktEIN Kraftanwendung getrennt durch seine Koordinaten eingestelltx,
beim,
z... Sie können die Stärke der Projektionen einstellenFx,
Fy,
Fzauf den Koordinatenachsen. Der Kraftmodul wird in diesem Fall durch die Formel bestimmt:
![]()
und die Richtungskosinus sind:
,
.
Analytische Art der Kräfteaddition : die Projektion des Vektors der Summe auf eine Achse ist gleich der algebraischen Summe der Projektionen der Terme der Vektoren auf derselben Achse, d. h. wenn:
dann , , .
Wissen Rx, Ry, Rz, wir können das Modul definieren
![]()
und Richtungskosinus:
, , .
Abbildung 1.9
Für das Gleichgewicht des Systems konvergierender Kräfte ist es notwendig und ausreichend, dass die Resultierende dieser Kräfte gleich Null ist.1) Geometrische Gleichgewichtsbedingung für ein konvergierendes Kräftesystem : für das Gleichgewicht des Systems konvergierender Kräfte ist es notwendig und ausreichend, dass das aus diesen Kräften gebildete Potenzpolygon,
geschlossen wurde (das Ende des Vektors des letzten Termes
Kraft muss mit dem Anfang des Vektors des ersten Termes der Kraft kombiniert werden). Dann ist der Hauptvektor des Kräftesystems gleich Null ()
2)
Analytische Gleichgewichtsbedingungen
.
Der Modul des Hauptvektors des Kräftesystems wird durch die Formel bestimmt.
![]() = 0. Soweit , dann kann der Wurzelausdruck nur dann gleich Null sein, wenn jeder Term gleichzeitig verschwindet, d.h.
= 0. Soweit , dann kann der Wurzelausdruck nur dann gleich Null sein, wenn jeder Term gleichzeitig verschwindet, d.h.
Rx= 0, Ry= 0, R z = 0.
Folglich ist es für das Gleichgewicht des räumlichen Systems konvergierender Kräfte notwendig und ausreichend, dass die Summen der Projektionen dieser Kräfte auf jede der drei Koordinaten der Achsen gleich Null sind:
Für das Gleichgewicht eines flachen Systems konvergierender Kräfte ist es notwendig und ausreichend, dass die Summen der Projektionen der Kräfte auf jede der beiden Koordinatenachsen gleich Null sind:
Die Addition zweier paralleler Kräfte, die in eine Richtung gerichtet sind.

Abbildung 1.9
Zwei parallele Kräfte, die in eine Richtung gerichtet sind, werden auf eine resultierende Kraft reduziert, die parallel zu ihnen und in die gleiche Richtung gerichtet ist. Die Größe der Resultierenden ist gleich der Summe der Größen dieser Kräfte, und ihr Angriffspunkt C teilt den Abstand zwischen den Wirkungslinien der Kräfte intern in Teile, die umgekehrt proportional zu den Größen dieser Kräfte sind, das istB A C
R = F 1 + F 2
Die Addition zweier ungleicher paralleler Kräfte, die in entgegengesetzte Richtungen gerichtet sind.
Zwei nicht gleich große antiparallele Kräfte werden auf eine zu ihnen parallele resultierende Kraft reduziert und auf die größere Kraft gerichtet. Der Betrag der Resultierenden ist gleich der Differenz der Beträge dieser Kräfte, und der Angriffspunkt C teilt den Abstand zwischen den Wirkungslinien der Kräfte äußerlich in Teile umgekehrt proportional zu den Größen dieser Kräfte, d. h.
Ein Kräftepaar und ein Kraftmoment relativ zu einem Punkt.
Ein Moment der Kraft
bezogen auf den Punkt O heißt mit entsprechendem Vorzeichen das Produkt aus der Größe der Kraft und dem Abstand h vom Punkt O zur Wirkungslinie der Kraft ... Dieses Produkt ist mit einem Pluszeichen gekennzeichnet, wenn die Stärke neigt dazu, den Körper gegen den Uhrzeigersinn zu drehen, und mit dem Vorzeichen - wenn die Kraft neigt dazu, den Körper im Uhrzeigersinn zu drehen, das heißt ... Die Länge der Senkrechten h heißtSchulter der Stärke
Punkt O. Wirkung der Krafteinwirkung, d.h. die Winkelbeschleunigung des Körpers ist umso größer, je größer das Kraftmoment ist.
Abbildung 1.11
Mit ein paar Stärken nennt man ein System, das aus zwei gleich großen parallelen Kräften besteht, die in entgegengesetzte Richtungen gerichtet sind. Der Abstand h zwischen den Kraftwirkungslinien heißtSchulterpaar . Ein Moment von ein paar Kräften m (F, F ") ist das Produkt der Größe einer der Kräfte, aus denen das Paar auf der Schulter des Paares besteht, mit dem entsprechenden Vorzeichen.Es wird wie folgt geschrieben: m (F, F") = ± F × h, wobei das Produkt mit einem Pluszeichen genommen wird, wenn ein Kräftepaar dazu neigt, den Körper gegen den Uhrzeigersinn zu drehen, und mit einem Minuszeichen, wenn ein Paar von Kräfte neigen dazu, den Körper im Uhrzeigersinn zu drehen.
Der Satz über die Summe der Momente der Kräfte eines Paares.
Die Summe der Kräftemomente des Paares (F, F ") relativ zu einem beliebigen Punkt 0, aufgenommen in der Wirkungsebene des Paares, hängt nicht von der Wahl dieses Punktes ab und ist gleich dem Moment des Paar.
Äquivalenter Paarsatz. Konsequenzen.
Satz. Zwei Paare, deren Momente einander gleich sind, sind äquivalent, d.h. (F, F") ~ (P, P")
Folgerung 1 ... Ein Kräftepaar kann an jede beliebige Stelle in seiner Wirkungsebene übertragen sowie in jedem Winkel gedreht werden und die Schulter und die Größe der Kräfte des Paares ändern, während das Moment des Paares beibehalten wird.
Folgerung 2. Ein Kräftepaar hat keine Resultierende und kann nicht durch eine in der Paarebene liegende Kraft ausgeglichen werden.

Abbildung 1.12
Addition und Gleichgewichtsbedingung für ein Paarsystem auf einer Ebene.
1. Der Satz über die Addition von Paaren, die in derselben Ebene liegen. Ein beliebig in derselben Ebene liegendes Paarsystem kann durch ein Paar ersetzt werden, dessen Moment gleich der Summe der Momente dieser Paare ist.
2. Ein Satz über das Gleichgewicht eines Paarsystems auf einer Ebene.
Damit ein absolut starrer Körper unter der Einwirkung eines beliebig in derselben Ebene liegenden Paares ruht, ist es notwendig und ausreichend, dass die Summe der Momente aller Paare gleich Null ist, d.h
Schwerpunkt
Schwere - die Resultierende der Anziehungskräfte auf die Erde, verteilt über das gesamte Körpervolumen.
Körperschwerpunkt - es ist ein solcher Punkt, der mit diesem Körper unweigerlich verbunden ist, durch den die Wirkungslinie der Schwerkraft dieses Körpers an jeder Stelle des Körpers im Raum verläuft.
Methoden zur Ermittlung des Schwerpunkts
1. Symmetriemethode:
1.1. Hat ein homogener Körper eine Symmetrieebene, so liegt der Schwerpunkt in dieser Ebene
1.2. Hat ein homogener Körper eine Symmetrieachse, so liegt der Schwerpunkt auf dieser Achse. Der Schwerpunkt eines gleichförmigen Rotationskörpers liegt auf der Rotationsachse.
1.3 Hat ein homogener Körper zwei Symmetrieachsen, so liegt der Schwerpunkt im Schnittpunkt der Symmetrieachsen.
2. Spaltverfahren: Der Körper wird in möglichst wenige Teile zerlegt, deren Schwerpunkte und Lage der Schwerpunkte bekannt sind.
3. Methode der negativen Massen: Bei der Bestimmung des Schwerpunkts eines Körpers mit freien Hohlräumen sollte die Methode der Aufteilung verwendet werden, jedoch sollte die Masse der freien Hohlräume als negativ betrachtet werden.
Koordinaten des Schwerpunkts einer ebenen Figur:

Die Lage der Schwerpunkte der einfachen geometrische Formen kann mit bekannten Formeln berechnet werden. (Abbildung 1.13)

Notiz: Der Schwerpunkt der Symmetrie der Figur liegt auf der Symmetrieachse.
Der Schwerpunkt der Stange liegt auf mittlerer Höhe.
1.2. Beispiele zur Lösung praktischer Probleme
Beispiel 1:
Die Last hängt an einer Stange und befindet sich im Gleichgewicht. Bestimmen Sie die Anstrengungen in der Stange. (Abbildung 1.2.1)
Lösung:
Die in den Befestigungsstangen auftretenden Kräfte sind gleich groß wie die Kräfte, mit denen die Stangen die Last tragen. (5. Axiom)
Wir bestimmen die möglichen Richtungen der Reaktionen der Bindungen "starre Stäbe".
Kräfte werden entlang der Stäbe geleitet.
Abbildung 1.2.1.
Lassen Sie uns Punkt A von Verbindungen befreien und die Aktion der Verbindungen durch ihre Reaktionen ersetzen. (Abbildung 1.2.2)
Wir beginnen die Konstruktion mit einer bekannten Kraft, indem wir den VektorFin gewisser Größenordnung.
Vom Ende des VektorsFziehe Linien parallel zu ReaktionenR 1 undR 2 .
Abbildung 1.2.2
Wenn sich Linien kreuzen, entsteht ein Dreieck. (Abbildung 1.2.3.). Wenn man den Maßstab der Konstruktionen kennt und die Länge der Seiten des Dreiecks misst, ist es möglich, die Größe der Reaktionen in den Stäben zu bestimmen.
Für genauere Berechnungen können Sie geometrische Beziehungen verwenden, insbesondere den Sinussatz: Das Verhältnis der Seite eines Dreiecks zum Sinus des entgegengesetzten Winkels ist ein konstanter Wert
![]()
Für diesen Fall:
Abbildung 1.2.3
![]()
Kommentar: Wenn die Richtung des Vektors (Bindungsreaktion) auf dem gegebenen Schema und im Kräftedreieck nicht übereinstimmt, sollte die Reaktion auf das Schema in die entgegengesetzte Richtung gerichtet sein.
Beispiel 2:
Bestimmen Sie Betrag und Richtung des resultierenden flachen Systems konvergierender Kräfte analytisch.
Lösung:
Abbildung 1.2.4
1. Bestimmen Sie die Projektion aller Kräfte des Systems auf Ox (Abbildung 1.2.4)Durch algebraisches Addieren der Projektionen erhalten wir die Projektion der Resultierenden auf die Ox-Achse.

Das Vorzeichen zeigt an, dass das Ergebnis nach links gerichtet ist.
2. Bestimmen Sie die Projektion aller Kräfte auf die Oy-Achse:
Durch algebraisches Addieren der Projektionen erhalten wir die Projektion der Resultierenden auf die Oy-Achse.
Das Vorzeichen zeigt an, dass die Resultierende nach unten gerichtet ist.
3. Bestimmen Sie den Modul der Resultierenden durch die Werte der Projektionen:
4. Bestimmen Sie den Wert des Winkels der Resultierenden mit der Ox-Achse:

und der Wert des Winkels mit der Oy-Achse:
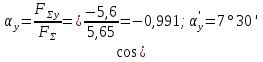
Beispiel 3:
Berechnen Sie die Summe der Kräftemomente relativ zum Punkt O (Bild 1.2.6).
OA= AB= VD = DE = CB = 2m
Abbildung 1.2.6
Lösung:
1. Das Kraftmoment relativ zu einem Punkt ist numerisch gleich dem Produkt aus Modul und Schulter der Kraft.
2. Das Kraftmoment ist gleich Null, wenn die Wirkungslinie der Kraft durch den Punkt geht.
Beispiel 4:
Bestimmen Sie die Position des Schwerpunkts der in Abbildung 1.2.7 gezeigten Figur
Lösung:
Wir teilen die Figur in drei auf:
1-Rechteck
EIN 1 = 10 * 20 = 200 cm 2
2-Dreieck
EIN 2 = 1/2 * 10 * 15 = 75cm 2
3-Kreis
EIN 3 =3,14*3 2 = 28,3 cm 2
Schwerpunkt von Abbildung 1: x 1 = 10cm, y 1 = 5cm
Schwerpunkt von Abbildung 2: x 2 = 20 + 1/3 * 15 = 25cm, y 2 = 1/3 * 10 = 3,3 cm
Schwerpunkt von Abbildung 3: x 3 = 10cm, y 3 = 5cm
In ähnlicher Weise Mit = 4,5 cm
Kinematik: Grundbegriffe.
Grundlegende kinematische Parameter
Flugbahn - eine Linie, die von einem materiellen Punkt umrissen wird, wenn man sich im Raum bewegt. Die Flugbahn kann gerade und gekrümmt, flach und räumlich sein.
Trajektoriengleichung für ebene Bewegung: y =F ( x)
Distanz zurückgelegt. Der Weg wird entlang des Wegs in Fahrtrichtung gemessen. Bezeichnung -S, Maßeinheiten - Meter.
Punktbewegungsgleichung Ist eine Gleichung, die die Position eines sich bewegenden Punktes als Funktion der Zeit bestimmt.
Abbildung 2.1
Die Position des Punktes zu jedem Zeitpunkt kann durch die Entfernung bestimmt werden, die entlang der Flugbahn von einem festen Punkt, der als Ursprung betrachtet wird, zurückgelegt wird (Abbildung 2.1). Diese Art der Bewegung wird genanntnatürlich ... Somit kann die Bewegungsgleichung als S = f (t) dargestellt werden.

Abbildung 2.2
Die Position eines Punktes kann auch bestimmt werden, wenn seine Koordinaten als Funktion der Zeit bekannt sind (Abbildung 2.2). Im Fall einer Bewegung auf einer Ebene müssen dann zwei Gleichungen angegeben werden:Bei räumlicher Bewegung kommt noch eine dritte Koordinate hinzuz= F 3 ( T)
Diese Art der Bewegungsangabe heißtKoordinate .
Reisegeschwindigkeit Ist eine Vektorgröße, die in . charakterisiert dieser Moment die Geschwindigkeit und Richtung der Bewegung entlang der Flugbahn.
Geschwindigkeit ist ein Vektor, der zu jedem Zeitpunkt tangential zur Trajektorie in Richtung der Bewegungsrichtung gerichtet ist (Abbildung 2.3).
Abbildung 2.3
Wenn ein Punkt in gleichen Zeiträumen gleiche Distanzen zurücklegt, dann heißt die BewegungUniform .Durchschnittsgeschwindigkeit auf dem Weg ΔSwird bestimmt durch:
woS- in der Zeit zurückgelegte Strecke ΔT; Δ T- Zeitintervall.
Wenn ein Punkt in gleichen Zeitabständen ungleiche Wege zurücklegt, heißt die Bewegungungleichmäßig ... In diesem Fall ist die Geschwindigkeit eine variable Größe und hängt von der Zeit abv= F( T)
Die momentane Geschwindigkeit ist definiert als
Punktbeschleunigung ist eine Vektorgröße, die die Geschwindigkeit der Geschwindigkeitsänderung in Betrag und Richtung charakterisiert.
Die Geschwindigkeit eines Punktes bei der Bewegung vom Punkt M1 zum Punkt Mg ändert sich in Größe und Richtung. Durchschnittliche Beschleunigung über diesen Zeitraum
Beschleunigung im Moment:
Normalerweise werden der Einfachheit halber zwei zueinander senkrechte Beschleunigungskomponenten betrachtet: Normale und Tangentiale (Abbildung 2.4)
Normalbeschleunigung a n , charakterisiert die Geschwindigkeitsänderung entlang
Richtung und ist definiert als
Die Normalbeschleunigung ist immer senkrecht zur Geschwindigkeit zum Mittelpunkt des Bogens.
Abbildung 2.4
Tangentialbeschleunigung a T , charakterisiert die Geschwindigkeitsänderung betragsmäßig und ist immer tangential zur Trajektorie gerichtet; beim Beschleunigen stimmt seine Richtung mit der Richtung der Geschwindigkeit überein, beim Verzögern ist er der Richtung des Geschwindigkeitsvektors entgegengesetzt.![]()
Der volle Beschleunigungswert ist definiert als:
Analyse der Bewegungsarten und kinematischen Parameter
Gleichmäßige Bewegung - diese Bewegung mit konstanter Geschwindigkeit:
Für eine gerade, gleichmäßige Bewegung:
Für geschwungene, gleichmäßige Bewegung:
![]()
Das Gesetz der gleichmäßigen Bewegung :
Äquivalente Bewegung – dies ist eine Bewegung mit konstanter Tangentialbeschleunigung:
Für geradlinige gleiche Bewegung
Für krummlinige gleichvariable Bewegung:
![]()
Das Gesetz der gleichen Bewegung:
![]()
Kinematische Grafiken
Kinematische Grafiken - Dies sind Diagramme der Änderungen von Weg, Geschwindigkeit und Beschleunigung gegenüber der Zeit.
Gleichmäßige Bewegung (Abbildung 2.5)

Abbildung 2.5
Äquivalente Bewegung (Abbildung 2.6)

Abbildung 2.6
Die einfachsten Bewegungen eines starren Körpers
Translationsbewegung heißt die Bewegung eines starren Körpers, bei der jede gerade Linie des Körpers während der Bewegung parallel zu seiner Ausgangsposition bleibt (Abbildung 2.7)

Abbildung 2.7
Bei der Translationsbewegung bewegen sich alle Punkte des Körpers gleich: Die Geschwindigkeiten und Beschleunigungen sind zu jedem Zeitpunkt gleich.
BeimDrehbewegung
alle Punkte des Körpers beschreiben einen Kreis um eine gemeinsame feste Achse.
Die feste Achse, um die sich alle Punkte des Körpers drehen, heißtDrehachse.
Um die Rotationsbewegung eines Körpers um eine feste Achse zu beschreiben, nurWinkelparameter. (Abbildung 2.8)
φ - der Drehwinkel des Körpers;
ω – Winkelgeschwindigkeit, bestimmt die Änderung des Drehwinkels pro Zeiteinheit;
Die zeitliche Änderung der Winkelgeschwindigkeit wird durch die Winkelbeschleunigung bestimmt:
2.2. Beispiele zur Lösung praktischer Probleme
Beispiel 1: Die Bewegungsgleichung eines Punktes ist gegeben. Bestimmen Sie die Geschwindigkeit des Punktes am Ende der dritten Bewegungssekunde und die durchschnittliche Geschwindigkeit der ersten drei Sekunden.
![]()
Lösung:
1. Geschwindigkeitsgleichung
2. Geschwindigkeit am Ende der dritten Sekunde (T=3 C)
3. Durchschnittsgeschwindigkeit
Beispiel 2: Bestimmen Sie nach dem gegebenen Bewegungsgesetz die Art der Bewegung, die Anfangsgeschwindigkeit und Tangentialbeschleunigung des Punktes, die Zeit bis zum Anhalten.
![]()
Lösung:
1. Bewegungsart: gleich variabel (![]() )
)
2. Beim Vergleich der Gleichungen fällt auf, dass
- der Anfangsweg, der vor Beginn der Zählung 10 m zurückgelegt wurde;
- Anfangsgeschwindigkeit 20m / s
- konstante Tangentialbeschleunigung ![]()
- die Beschleunigung ist negativ, daher wird die Bewegung verlangsamt, die Beschleunigung ist der Bewegungsgeschwindigkeit entgegengesetzt.
3. Sie können den Zeitpunkt definieren, zu dem die Geschwindigkeit des Punktes Null beträgt.
3.Dynamik: Grundkonzepte und Axiome
Dynamik - ein Abschnitt der theoretischen Mechanik, in dem ein Zusammenhang zwischen der Bewegung von Körpern und den auf sie einwirkenden Kräften hergestellt wird.
In der Dynamik werden zwei Arten von Problemen gelöst:
die Bewegungsparameter für gegebene Kräfte bestimmen;
Bestimmen Sie die auf den Körper wirkenden Kräfte nach den gegebenen kinematischen Bewegungsparametern.
Untermaterieller Punkt
implizieren einen bestimmten Körper, der eine bestimmte Masse hat (d. h. eine bestimmte Menge an Materie enthält), aber keine linearen Abmessungen hat (ein unendlich kleines Raumvolumen).
Isoliert
es wird ein Materialpunkt berücksichtigt, der nicht von anderen Materialpunkten beeinflusst wird. In der realen Welt gibt es keine isolierten materiellen Punkte wie isolierte Körper, dieses Konzept ist bedingt.
Während der Translationsbewegung bewegen sich alle Punkte des Körpers auf die gleiche Weise, sodass der Körper als materieller Punkt angesehen werden kann.
Wenn die Abmessungen des Körpers im Vergleich zur Flugbahn klein sind, kann er auch als materieller Punkt angesehen werden, während der Punkt mit dem Schwerpunkt des Körpers zusammenfällt.
Während der Rotationsbewegung des Körpers können sich die Punkte nicht gleich bewegen, in diesem Fall können einige Bestimmungen der Dynamik nur auf einzelne Punkte angewendet werden und das materielle Objekt kann als eine Menge materieller Punkte betrachtet werden.
Daher wird die Dynamik in die Dynamik des Punktes und die Dynamik des materiellen Systems unterteilt.
Axiome der Dynamik
Das erste Axiom ( Trägheitsprinzip): in Jeder isolierte Materialpunkt befindet sich in einem Zustand der Ruhe oder einer gleichmäßigen und geradlinigen Bewegung, bis die aufgebrachten Kräfte ihn aus diesem Zustand herausholen.
Dieser Zustand wird als Staat bezeichnetTrägheit. Entfernen Sie den Punkt aus diesem Zustand, d.h. um ihr etwas Beschleunigung zu verleihen, kann eine äußere Kraft erfolgen.
Jeder Körper (Punkt) besitztTrägheit. Die Körpermasse ist ein Maß für die Trägheit.
Nach Gewicht werden genanntdie Stoffmenge im Körpervolumen, in der klassischen Mechanik gilt er als konstanter Wert. Die Maßeinheit für die Masse ist Kilogramm (kg).
Zweites Axiom (Das zweite Newtonsche Gesetz ist das Grundgesetz der Dynamik)
F = ma
woT - Punktmasse, kg;ein - Punktbeschleunigung, m / s 2 .
Die durch Kraft auf einen materiellen Punkt ausgeübte Beschleunigung ist proportional zur Größe der Kraft und stimmt mit der Kraftrichtung überein.
Die Schwerkraft wirkt auf alle Körper der Erde, sie verleiht dem Körper die auf den Erdmittelpunkt gerichtete Gravitationsbeschleunigung:
G = mg,
wog - 9,81 m / s², Erdbeschleunigung.
Drittes Axiom (Newtons drittes Gesetz): cSchlicke der Wechselwirkung zweier Körper sind gleich groß und entlang einer Geraden in verschiedene Richtungen gerichtet.
Bei der Wechselwirkung sind Beschleunigungen umgekehrt proportional zu Massen.
Viertes Axiom (das Gesetz der Unabhängigkeit der Kraftwirkung): toJede Kraft eines Kräftesystems wirkt so, als würde sie allein wirken.
Die vom Kräftesystem auf den Punkt ausgeübte Beschleunigung ist gleich der geometrischen Summe der Beschleunigungen, die jede Kraft einzeln auf den Punkt aufbringt (Abbildung 3.1):

Abbildung 3.1
Reibungskonzept. Arten von Reibung.
Reibung-
Widerstand, der sich aus der Bewegung eines rauen Körpers auf der Oberfläche eines anderen ergibt. Beim Gleiten von Körpern entsteht Gleitreibung, beim Rollen - Schwingreibung.
Gleitreibung
Abbildung 3.2.
Der Grund ist der mechanische Eingriff der Vorsprünge. Die Kraft des Bewegungswiderstands beim Gleiten wird als Gleitreibungskraft bezeichnet (Abbildung 3.2).Gleitreibungsgesetze:
1. Die Gleitreibungskraft ist direkt proportional zur normalen Druckkraft: 
woR- Normaldruckkraft, senkrecht zur Auflagefläche gerichtet;F- Gleitreibungskoeffizient.
Abbildung 3.3.
Bei Körperbewegungen entlang schiefe Ebene(Abbildung 3.3)Rollreibung
Der Rollwiderstand ist mit einer gegenseitigen Verformung des Bodens und des Rades verbunden und bedeutet deutlich weniger Gleitreibung.
Für ein gleichmäßiges Rollen der Räder muss Kraft aufgewendet werdenF dv (Abbildung 3.4)
Die Rollbedingung des Rades ist, dass das Bewegungsmoment nicht kleiner als das Widerstandsmoment sein darf:
Abbildung 3.4.
Beispiel 1: Beispiel 2: Zu zwei materiellen Punkten mit Massem 1 = 2kg undm 2 = 5 kg werden die gleichen Kräfte aufgebracht. Vergleichen Sie die Werte schneller.Lösung:
Nach dem dritten Axiom ist die Beschleunigungsdynamik umgekehrt proportional zu den Massen: ![]()
Beispiel 3:
Bestimmen Sie die Schwerkraftarbeit beim Bewegen der Last von Punkt A nach Punkt C entlang einer schiefen Ebene (Abbildung 3.7). Die Schwerkraft des Körpers beträgt 1500 N. AB = 6 m, BC = 4 m. Beispiel 3:
Bestimmen Sie die Arbeit der Schnittkraft in 3 min. Werkstückdrehzahl 120 U/min, Werkstückdurchmesser 40 mm, Schnittkraft 1 kN. (Abbildung 3.8)
Lösung:
1. Arbeiten in Drehbewegung:
2. Winkelgeschwindigkeit 120 U/min
Abbildung 3.8.
3. Die Anzahl der Umdrehungen für eine bestimmte Zeit istz= 120 * 3 = 360 UmdrehungenDer Drehwinkel während dieser Zeit beträgt φ = 2πz= 2 * 3,14 * 360 = 2261rad
4. Arbeiten Sie in 3 Runden:W= 1 * 0,02 * 2261 = 45,2 kJ
Referenzliste
Olofinskaya, V. P. "Technische Mechanik", Moskauer "Forum" 2011
Erdedi A.A. Erdedi N.A. Theoretische Mechanik. Materialbeständigkeit.- Rn-D; Phönix, 2010
Vorlesungen zur theoretischen Mechanik
Punktdynamik
Vorlesung 1
Grundbegriffe der Dynamik
Im Kapitel Dynamik die Bewegung von Körpern unter Einwirkung von Kräften wird untersucht. Daher wird zusätzlich zu den Konzepten, die im Abschnitt . vorgestellt wurden, Kinematik, hier ist es notwendig, neue Konzepte zu verwenden, die die Besonderheiten der Wirkung von Kräften auf verschiedene Körper und die Reaktion von Körpern auf diese Einflüsse widerspiegeln. Betrachten wir die wichtigsten dieser Konzepte.
eine Stärke
Kraft ist ein quantitatives Ergebnis des Aufpralls anderer Körper auf einen bestimmten Körper. Kraft ist eine Vektorgröße (Abb. 1).
![]()
![]()
Punkt A des Anfangs des Kraftvektors F namens Kraftangriffspunkt... Die Gerade MN, auf der der Kraftvektor liegt, heißt Wirkungslinie der Kraft. Die Länge eines Kraftvektors, gemessen in einem bestimmten Maßstab, heißt Zahlenwert oder Modul des Kraftvektors... Der Kraftmodul wird als oder bezeichnet. Die Krafteinwirkung auf den Körper äußert sich entweder in ihrer Verformung, wenn der Körper bewegungslos ist, oder in einer Beschleunigung, wenn sich der Körper bewegt. Auf diesen Kraftäußerungen basiert die Einrichtung verschiedener Geräte (Kraftmesser oder Dynamometer) zur Messung von Kräften.
b) Kräftesystem
Die betrachtete Kräftemenge bildet System der Kräfte. Jedes aus n Kräften bestehende System kann in der folgenden Form geschrieben werden: ![]()
c) freier Körper
Ein Körper, der sich im Raum in jede Richtung bewegen kann, ohne eine direkte (mechanische) Wechselwirkung mit anderen Körpern zu erfahren, heißt kostenlos oder isoliert... Die Wirkung des einen oder anderen Kräftesystems auf einen Körper kann nur geklärt werden, wenn dieser Körper frei ist.
d) resultierende Kraft
Wenn eine Kraft auf einen freien Körper die gleiche Wirkung wie ein bestimmtes Kräftesystem ausübt, dann heißt diese Kraft die Resultierende dieses Kräftesystems... Dies ist wie folgt geschrieben:
![]() ,
,
was bedeutet Gleichwertigkeit Wirkung auf ein und denselben freien Körper der resultierenden und eines Systems von n Kräften.
Betrachten wir nun komplexere Konzepte zur quantitativen Bestimmung der Rotationswirkungen von Kräften.
e) Kraftmoment um einen Punkt (Mitte)
Kann sich der Körper unter Krafteinwirkung um einen Fixpunkt O drehen (Abb. 2), so führt man zur Quantifizierung dieses Rotationseffekts eine physikalische Größe ein, die als bezeichnet wird Kraftmoment um einen Punkt (Mitte).

Die Ebene, die durch einen gegebenen Fixpunkt und die Wirkungslinie der Kraft geht, heißt Kraftwirkungsebene... In Abb. 2 ist dies die Ebene .
Das Kraftmoment relativ zu einem Punkt (Mitte) ist eine Vektorgröße gleich dem Vektorprodukt des Radiusvektors des Kraftangriffspunktes durch den Kraftvektor:
![]() ( 1)
( 1)
Nach der Regel der Vektormultiplikation zweier Vektoren ist ihr Vektorprodukt ein Vektor senkrecht zur Ortsebene der Vektoren der Faktoren (in diesem Fall der Ebene des Dreiecks OAB), der in die Richtung gerichtet ist, aus der die kürzeste Drehung des ersten Vektors des Faktors zum zweiten Vektor ist der Faktor gegen den Uhrzeiger sichtbar (Abb. 2). Mit dieser Ordnung der Vektoren der Faktoren des Vektorprodukts (1) wird die Drehung des Körpers unter Krafteinwirkung gegen den Uhrzeiger sichtbar (Abb. 2) Da der Vektor senkrecht zur Wirkungsebene steht der Kraft bestimmt ihre Lage im Raum die Lage der Wirkungsebene der Kraft relativ zum Zentrum ist gleich der verdoppelten Fläche ОАВ und lässt sich nach folgender Formel bestimmen:
![]() ,
(2)
,
(2)
wo Größeh, gleich dem kürzesten Abstand von einem gegebenen Punkt O zur Wirkungslinie der Kraft, heißt Schulter der Kraft.
Ist die Lage der Kraftwirkungsebene im Raum für die Kennlinie der Drehwirkung der Kraft nicht wesentlich, so ist in diesem Fall statt des Kraftmomentvektors die Drehwirkung der Kraft zu charakterisieren wird genutzt algebraisches Kraftmoment:
![]() (3)
(3)
Das algebraische Kraftmoment relativ zu einem gegebenen Zentrum ist gleich dem Produkt des Kraftmoduls durch seine Schulter, genommen mit einem Plus- oder Minuszeichen. Dabei entspricht das positive Moment der Drehung des Körpers unter Einwirkung der gegebenen Kraft gegen den Uhrzeiger und das negative Moment der Drehung des Körpers entlang des Uhrzeigers. Aus den Formeln (1), (2) und (3) folgt das Kraftmoment relativ zum Punkt ist nur dann null, wenn die Schulter dieser Krafthgleich null... Eine solche Kraft kann den Körper nicht um einen bestimmten Punkt drehen.
f) Kraftmoment um die Achse
Wenn sich der Körper unter Krafteinwirkung um eine feste Achse drehen kann (z. B. die Drehung eines Tür- oder Fensterrahmens in Scharnieren beim Öffnen oder Schließen), dann wird zur Quantifizierung dieses Rotationseffekts eine physikalische Größe eingeführt, die wird genannt Kraftmoment um eine gegebene Achse.
 z
z
B F xy
Bild 3 zeigt ein Diagramm, nach dem das Kraftmoment relativ zur z-Achse bestimmt wird:
Der Winkel wird durch zwei senkrechte Richtungen z und zu den Dreiecksebenen O . gebildet ab bzw. OAV. Seit O ab die Projektion von ОАВ auf die xy-Ebene ist, dann gilt nach dem Stereometriesatz über die Projektion einer ebenen Figur auf diese Ebene:
wobei das Pluszeichen dem positiven Wert von cos entspricht, d. h. den spitzen Winkeln , und das Minuszeichen dem negativen Wert von cos entspricht, d. h. den stumpfen Winkeln , was auf die Richtung des Vektors zurückzuführen ist. SO . wiederum ab=1/2abh, wo h ab ... Segmentgröße ab gleich der Projektion der Kraft auf die xy-Ebene, d.h. . ab = F xy .
Basierend auf dem Obigen sowie den Gleichungen (4) und (5) definieren wir das Kraftmoment relativ zur z-Achse wie folgt:
Gleichung (6) erlaubt es uns, die folgende Definition des Kraftmoments relativ zu einer beliebigen Achse zu formulieren: Das Kraftmoment relativ zu einer gegebenen Achse ist gleich der Projektion des Vektors des Moments dieser Kraft relativ zu einer beliebigen Achse auf diese Achse Punkt dieser Achse und ist definiert als das Produkt der Projektion der Kraft auf die Ebene senkrecht zu dieser Achse, genommen mit einem Plus- oder Minuszeichen auf der Schulter dieser Projektion relativ zum Schnittpunkt der Achse mit der Projektionsebene . In diesem Fall gilt das Vorzeichen des Moments als positiv, wenn aus positiver Richtung der Achse gesehen die Drehung des Körpers um diese Achse gegen den Uhrzeiger sichtbar ist. Andernfalls wird das Kraftmoment um die Achse negativ genommen. Da sich diese Definition des Kraftmoments um die Achse nur schwer einprägen lässt, empfiehlt es sich, sich die Formel (6) und Abb. 3 zu merken, die diese Formel erklärt.
Aus Formel (6) folgt, dass das Kraftmoment um die Achse ist null, wenn sie ist parallel zur Achse (in diesem Fall ist ihre Projektion auf eine Ebene senkrecht zur Achse Null), oder die Wirkungslinie der Kraft schneidet die Achse (dann die Schulter der Projektion h=0). Dies entspricht voll und ganz der physikalischen Bedeutung des Kraftmoments um die Achse als quantitative Kenngröße der Drehwirkung der Kraft auf einen Körper mit Drehachse.
g) Körpergewicht
Es ist seit langem bekannt, dass ein Körper unter Krafteinwirkung allmählich an Geschwindigkeit gewinnt und sich weiterbewegt, wenn die Kraft weggenommen wird. Diese Eigenschaft von Körpern, sich einer Veränderung ihrer Bewegung zu widersetzen, wurde als . bezeichnet Trägheit oder Trägheit von Körpern. Das quantitative Maß für die Trägheit eines Körpers ist seine Masse. Außerdem, Körpermasse ist ein quantitatives Maß für die Wirkung von Gravitationskräften auf einen bestimmten Körper je größer die Masse des Körpers, desto größer die auf den Körper wirkende Gravitationskraft. Wie nachfolgend dargestellt, äh Diese beiden Definitionen des Körpergewichts hängen zusammen.
Die restlichen Konzepte und Definitionen von Dynamik werden später in den Abschnitten besprochen, in denen sie zum ersten Mal erscheinen.
2. Bindungen und Bindungsreaktionen
Zuvor in Abschnitt 1 Buchstabe (c) wurde der Begriff eines freien Körpers angegeben, als ein Körper, der sich im Raum in jede Richtung bewegen kann, ohne in direktem Kontakt mit anderen Körpern zu stehen. Die meisten realen Körper, die uns umgeben, stehen in direktem Kontakt mit anderen Körpern und können sich nicht in die eine oder andere Richtung bewegen. So können sich beispielsweise Körper auf der Tischoberfläche in jede beliebige Richtung bewegen, außer der Richtung senkrecht zur Tischoberfläche nach unten. An Scharnieren befestigte Türen können sich drehen, aber nicht translatorisch bewegen usw. Körper, die sich im Raum nicht in die eine oder andere Richtung bewegen können, werden als . bezeichnet nicht frei.
Alles, was die Bewegung eines bestimmten Körpers im Raum einschränkt, wird als Beschränkung bezeichnet. Es können alle anderen Körper sein, die die Bewegung dieses Körpers in einige Richtungen verhindern ( physische Verbindungen); im weiteren Sinne können es einige Bedingungen sein, die der Bewegung des Körpers auferlegt werden und diese Bewegung einschränken. Sie können also eine Bedingung stellen, dass die Bewegung eines Materialpunkts entlang einer bestimmten Kurve erfolgt. In diesem Fall wird die Verbindung mathematisch in Form einer Gleichung ( Beschränkungsgleichung). Auf die Frage nach den Arten von Verknüpfungen wird im Folgenden näher eingegangen.
Die meisten der Körpern auferlegten Verbindungen sind praktisch physikalische Verbindungen. Daher stellt sich die Frage nach der Interaktion dieses Körpers und der diesem Körper auferlegten Verbindung. Diese Frage beantwortet das Axiom über die Wechselwirkung von Körpern: Zwei Körper wirken mit gleich großen, entgegengesetzten Kräften aufeinander ein und liegen auf derselben Geraden. Diese Kräfte werden Wechselwirkungskräfte genannt. Wechselwirkungskräfte werden auf verschiedene interagierende Körper ausgeübt. Wenn also beispielsweise ein bestimmter Körper und eine Verbindung zusammenwirken, wird eine der Wechselwirkungskräfte von der Seite des Körpers auf die Verbindung ausgeübt und die andere Wechselwirkungskraft wird von der Seite der Verbindung auf diesen Körper ausgeübt. Diese letzte Macht heißt durch die Stärke der Bindungsreaktion oder einfach, kommunikative Reaktion.
Bei der Lösung praktischer dynamischer Probleme ist es notwendig, die Richtung von Reaktionen zu finden verschiedene Typen Verbindungen. Dabei kann manchmal die allgemeine Regel zur Bestimmung der Richtung der Bindungsreaktion helfen: Die Bindungsreaktion ist immer entgegengesetzt zu der Richtung gerichtet, in der diese Bindung die Bewegung des gegebenen Körpers verhindert. Wenn diese Richtung eindeutig angegeben werden kann, wird die Reaktion der Verbindung durch die Richtung bestimmt. Ansonsten ist die Richtung der Bindungsreaktion unsicher und kann nur aus den entsprechenden Bewegungsgleichungen bzw. Gleichgewichten des Körpers ermittelt werden. Die Frage nach den Verbindungsarten und der Richtung ihrer Reaktionen sollte genauer im Lehrbuch untersucht werden: S.M. Targ Ein kurzer Kurs in theoretischer Mechanik "Gymnasium", M., 1986. Kapitel 1, §3.
In Abschnitt 1 Buchstabe c wurde gesagt, dass die Wirkung eines Kräftesystems nur dann vollständig bestimmt werden kann, wenn dieses Kräftesystem auf einen freien Körper aufgebracht wird. Da die meisten Körper in Wirklichkeit nicht frei sind, stellt sich zur Untersuchung der Bewegung dieser Körper die Frage, wie diese Körper frei gemacht werden können. Diese Frage ist beantwortet Axiom der Vorlesungsverbindungen an Philosophie zu Hause. Vorträge waren ... Sozialpsychologie und Ethnopsychologie. 3. Theoretisch Ergebnisse Im Sozialdarwinismus gab es ...
Theoretisch Mechanik
Studienführer >> PhysikAbstrakt Vorträge an Gegenstand THEORETISCH MECHANIK Für Studierende der Fachrichtung: 260501.65 ... - Vollzeit Abstract Vorträge zusammengestellt auf der Grundlage von: L. V. Butorin, E. B. Busygin. Theoretisch Mechanik... Übungsanleitung ...
1 Folie
Vorlesungen über Theoretische Mechanik Dynamik (I-Teil) Bondarenko A.N. Moskau - 2007 Elektronik Trainingskurs geschrieben auf der Grundlage von Vorlesungen des Autors für Studenten, die in den Fachgebieten SZD, PGS und SDM an NIIZhT und MIIT (1974-2006) studiert haben. Studienmaterial entspricht Kalenderpläne im Umfang von drei Semestern. Um Animationseffekte während einer Präsentation vollständig zu implementieren, müssen Sie einen Power Point-Viewer verwenden, der nicht niedriger als das integrierte Microsoft Office ist Betriebssystem Windows-XP-Profi. Kommentare und Anregungen können per E-Mail gesendet werden: [E-Mail geschützt]... Moskowski Staatliche Universität Eisenbahn (MIIT) Institut für Theoretische Mechanik Wissenschaftliches und Technisches Zentrum für Verkehrstechnologien

2 rutsche
Inhalt Vorlesung 1. Einführung in die Dynamik. Gesetze und Axiome der Dynamik eines materiellen Punktes. Grundgleichung der Dynamik. Differential- und natürliche Bewegungsgleichungen. Zwei Hauptaufgaben der Dynamik. Beispiele zur Lösung des direkten Problems der Dynamik Vorlesung 2. Lösung des inversen Problems der Dynamik. Allgemeine Anleitung zur Lösung des inversen Dynamikproblems. Beispiele zur Lösung des inversen Problems der Dynamik. Die Bewegung eines schräg zum Horizont geworfenen Körpers ohne Berücksichtigung des Luftwiderstands. Vorlesung 3. Geradlinige Schwingungen eines materiellen Punktes. Voraussetzung für das Auftreten von Schwingungen. Klassifizierung von Schwingungen. Freie Schwingungen ohne Berücksichtigung der Widerstandskräfte. Gedämpfte Schwingungen. Verringerung von Schwankungen. Vorlesung 4. Erzwungene Schwingungen eines materiellen Punktes. Resonanz. Der Einfluss des Bewegungswiderstandes bei erzwungenen Schwingungen. Vorlesung 5. Relative Bewegung eines materiellen Punktes. Trägheitskräfte. Besondere Bewegungsfälle für verschiedene Arten von tragbaren Bewegungen. Der Einfluss der Erdrotation auf das Gleichgewicht und die Bewegung von Körpern. Vorlesung 6. Dynamik eines mechanischen Systems. Mechanisches System. Äußere und innere Kräfte. Der Massenschwerpunkt des Systems. Der Satz über die Bewegung des Massenschwerpunkts. Naturschutzgesetze. Ein Beispiel für die Lösung eines Problems mit dem Satz über die Bewegung des Massenschwerpunkts. Vortrag 7. Machtimpuls. Die Menge an Bewegung. Das Theorem über die Änderung des Bewegungsbetrages. Naturschutzgesetze. Satz von Euler. Ein Beispiel zur Lösung des Problems der Anwendung des Satzes über die Impulsänderung. Moment der Dynamik. Satz über die Änderung des Drehimpulses .. Vorlesung 8. Erhaltungssätze. Elemente der Theorie der Trägheitsmomente. Kinetisches Moment eines starren Körpers. Differentialgleichung der Rotation eines starren Körpers. Ein Beispiel zur Lösung des Problems zur Anwendung des Satzes über die Änderung des Drehimpulses des Systems. Elementare Theorie des Kreisels. Leseempfehlung 1. Yablonskiy A.A. Studiengang Theoretische Mechanik. Teil 2. M.: Gymnasium. 1977 368 s. 2. Meschtscherski I. V. Sammlung von Problemen der theoretischen Mechanik. M.: Wissenschaft. 1986 416 s. 3. Sammlung von Hausarbeiten für Hausarbeiten / Ed. A. A. Jablonski. M.: Gymnasium. 1985 366 S. 4. Bondarenko A. N. „Theoretische Mechanik in Beispielen und Problemen. Dynamik ”(elektronisches Handbuch www.miit.ru/institut/ipss/faculties/trm/main.htm), 2004

3 rutsche
Vorlesung 1 Dynamik ist ein Teilgebiet der theoretischen Mechanik, das die mechanische Bewegung vom allgemeinsten Standpunkt aus untersucht. Die Bewegung wird im Zusammenhang mit den auf das Objekt einwirkenden Kräften betrachtet. Der Abschnitt besteht aus drei Abschnitten: Dynamik eines materiellen Punktes Dynamik Dynamik eines mechanischen Systems Analytische Mechanik ■ Dynamik eines Punktes - untersucht die Bewegung eines materiellen Punktes unter Berücksichtigung der diese Bewegung verursachenden Kräfte. Das Hauptobjekt ist ein materieller Punkt - ein materieller Körper mit einer Masse, dessen Abmessungen vernachlässigt werden können. Grundannahmen: - es gibt einen absoluten Raum (er hat rein geometrische Eigenschaften, die nicht von Materie und ihrer Bewegung abhängen. - es gibt eine absolute Zeit (hängt nicht von Materie und ihrer Bewegung ab). Daraus folgt: - es gibt ein absolut bewegungsloses Bezugssystem - die Zeit hängt nicht von der Bewegung des Bezugssystems ab - die Massen der bewegten Punkte hängen nicht von der Bewegung des Bezugssystems ab Diese Annahmen werden in der klassischen Mechanik verwendet, die von Galileo und Newton erstellt wurde Es hat noch ein ziemlich breites Anwendungsgebiet, da die in der angewandten Wissenschaften betrachteten mechanischen Systeme nicht so große Massen und Bewegungsgeschwindigkeiten aufweisen, für die der Einfluss auf die Geometrie von Raum, Zeit, Bewegung berücksichtigt werden muss , wie es in der relativistischen Mechanik (Relativitätstheorie) der Fall ist, ihre dynamische Wechselwirkung Aktionen unter dem Einfluss verschiedener Kräfte. ■ Das Trägheitsgesetz (Galileo-Newton-Gesetz) - Als isolierter materieller Punkt behält der Körper seinen Ruhezustand oder seine gleichförmige geradlinige Bewegung bei, bis die aufgebrachten Kräfte ihn zwingen, diesen Zustand zu ändern. Dies impliziert die Äquivalenz von Ruhe- und Bewegungszustand durch Trägheit (Galileis Relativitätsgesetz). Der Bezugsrahmen, für den das Trägheitsgesetz erfüllt ist, wird Trägheit genannt. Die Eigenschaft eines materiellen Punktes, die Geschwindigkeit seiner Bewegung (seinen kinematischen Zustand) unverändert zu halten, wird als Trägheit bezeichnet. ■ Das Gesetz der Proportionalität von Kraft und Beschleunigung (Grundgleichung der Dynamik - Newtons II. Gesetz) - Die durch Kraft auf einen materiellen Punkt ausgeübte Beschleunigung ist direkt proportional zur Kraft und umgekehrt proportional zur Masse dieses Punktes: oder Hier ist m die Masse des Punktes (Trägheitsmaß), gemessen in kg, numerisch gleiches Gewicht geteilt durch die Erdbeschleunigung: F ist die wirkende Kraft, gemessen in N (1 N bewirkt eine Beschleunigung von 1 m / s2 auf einen Punkt mit a Masse von 1 kg, 1 N = 1/9. 81 kg-s). ■ Dynamik eines mechanischen Systems - untersucht die Bewegung einer Reihe von materiellen Punkten und Festkörpern, die durch allgemeine Wechselwirkungsgesetze verbunden sind, unter Berücksichtigung der Kräfte, die diese Bewegung verursachen. ■ Analytische Mechanik - untersucht die Bewegung nicht-freier mechanischer Systeme mit allgemeinen analytischen Methoden. eins

4 rutsche
Vorlesung 1 (Fortsetzung - 1.2) Bewegungsdifferentialgleichungen eines materiellen Punktes: - Bewegungsdifferentialgleichungen eines Punktes in Vektorform. - Differentialgleichungen der Bewegung eines Punktes in Koordinatenform. Dieses Ergebnis kann durch formale Projektion der Vektor-Differentialgleichung (1) erhalten werden. Nach der Gruppierung zerfällt die Vektorrelation in drei Skalargleichungen: In Koordinatenform: Wir verwenden die Beziehung des Radiusvektors mit Koordinaten und des Kraftvektors mit Projektionen: oder: Ersetze die Beschleunigung eines Punktes in der vektoriellen Bewegungseinstellung in die Grundgleichung der Dynamik: Natürliche Bewegungsgleichungen eines materiellen Punktes erhält man durch Projektion einer vektoriellen Bewegungsdifferentialgleichung auf natürliche (bewegliche) Koordinatenachsen: oder: - natürliche Bewegungsgleichungen eines Punktes. ■ Die Grundgleichung der Dynamik: - entspricht der Vektormethode zur Angabe der Bewegung eines Punktes. ■ Das Gesetz der Unabhängigkeit der Kraftwirkung - Die Beschleunigung eines materiellen Punktes unter der Wirkung mehrerer Kräfte ist gleich der geometrischen Summe der Beschleunigungen eines Punktes von der Wirkung jeder der Kräfte getrennt: oder das Gesetz gilt für jeden kinematischen Zustand von Körpern. Die Wechselwirkungskräfte, die auf verschiedene Punkte (Körper) ausgeübt werden, sind nicht ausgeglichen. ■ Gesetz der Gleichheit von Wirkung und Reaktion (III. Newtonsches Gesetz) - Jede Aktion entspricht einer gleich großen und entgegengesetzt gerichteten Reaktion: 2

5 Folie
Zwei Hauptprobleme der Dynamik: 1. Direktes Problem: Bewegung ist gegeben (Bewegungsgleichungen, Trajektorie). Es ist erforderlich, die Kräfte zu bestimmen, unter deren Wirkung eine bestimmte Bewegung auftritt. 2. Inverses Problem: Die Kräfte, unter deren Wirkung die Bewegung auftritt. Es ist erforderlich, die Bewegungsparameter (Bewegungsgleichungen, Bewegungsbahn) zu finden. Beide Probleme werden mit der Grundgleichung der Dynamik und deren Projektion auf die Koordinatenachsen gelöst. Betrachtet man die Bewegung eines nicht freien Punktes, so kommt wie in der Statik das Prinzip der Bindungsfreiheit zur Anwendung. Durch die Reaktion gehen die Bindungen in die Zusammensetzung der auf den Materialpunkt einwirkenden Kräfte ein. Die Lösung des ersten Problems ist mit Differenzierungsoperationen verbunden. Die Lösung des inversen Problems erfordert die Integration der entsprechenden Differentialgleichungen, und dies ist viel schwieriger als die Differenzierung. Das inverse Problem ist komplizierter als das direkte Problem. Betrachten wir die Lösung des direkten Dynamikproblems anhand von Beispielen: Beispiel 1. Eine Aufzugskabine mit dem Gewicht G wird an einem Seil mit der Beschleunigung a angehoben. Bestimmen Sie die Kabelspannung. 1. Wir wählen ein Objekt aus (die Aufzugskabine bewegt sich progressiv und kann als materieller Punkt betrachtet werden). 2. Wir verwerfen die Verbindung (Kabel) und ersetzen durch Reaktion R. 3. Stellen Sie die Grundgleichung der Dynamik auf: Bestimmen Sie die Reaktion des Kabels: Bestimmen Sie die Spannung des Kabels: Bei gleichförmiger Bewegung des Fahrerhauses ay = 0 und die Spannung des Kabels ist gleich dem Gewicht: T = G. Wenn das Kabel reißt, ist T = 0 und die Beschleunigung der Kabine ist gleich der Erdbeschleunigung: ay = -g. 3 4. Projizieren wir die Grundgleichung der Dynamik auf die y-Achse: y Beispiel 2. Ein Massepunkt m bewegt sich entlang einer horizontalen Fläche (Oxy-Ebene) nach den Gleichungen: x = a coskt, y = b coskt. Bestimmen Sie die Kraft, die auf den Punkt einwirkt. 1. Wählen Sie ein Objekt (Materialpunkt) aus. 2. Wir verwerfen die Verbindung (Ebene) und ersetzen sie durch die Reaktion N. 3. Wir fügen dem Kräftesystem eine unbekannte Kraft F hinzu 4. Wir stellen die Grundgleichung der Dynamik auf: 5. Wir projizieren die Grundgleichung der Dynamik auf x, y-Achsen: Bestimmen Sie die Projektion der Kraft: Kraftmodul: Richtungskosinus: Der Betrag der Kraft ist also proportional zum Abstand des Punktes zum Koordinatenmittelpunkt und wird entlang der Verbindungslinie zwischen Punkt und Mittelpunkt zum Mittelpunkt gerichtet . Die Trajektorie eines Punktes ist eine Ellipse, die im Ursprung zentriert ist: O r Vorlesung 1 (Fortsetzung - 1.3)

6 rutsche
Vorlesung 1 (Fortsetzung 1.4) Beispiel 3: Eine Last mit dem Gewicht G hängt an einem Seil der Länge l und bewegt sich mit einer bestimmten Geschwindigkeit auf einer Kreisbahn in der horizontalen Ebene. Der Abweichungswinkel des Kabels von der Vertikalen ist gleich. Bestimmen Sie die Seilspannung und die Lastgeschwindigkeit. 1. Wählen Sie das Objekt (Fracht) aus. 2. Wir verwerfen die Verbindung (Kabel) und ersetzen durch Reaktion R. 3. Stellen Sie die Grundgleichung der Dynamik auf: Aus der dritten Gleichung bestimmen wir die Reaktion des Kabels: Wir bestimmen die Spannung des Kabels: Ersetzen Sie den Wert von Seilreaktion, Normalbeschleunigung in die zweite Gleichung und bestimmen Sie die Geschwindigkeit der Last: 4. Projizieren Sie die Grundgleichung Dynamik auf die Achse, n, b: Beispiel 4: Ein Auto mit Gewicht G bewegt sich auf einer konvexen Brücke (Krümmungsradius ist R) bei einer Geschwindigkeit V. Bestimmen Sie den Druck des Autos auf der Brücke. 1. Wir wählen ein Objekt aus (ein Auto, wir vernachlässigen die Abmessungen und betrachten es als Punkt). 2. Wir verwerfen die Bindung (raue Oberfläche) und ersetzen durch Reaktionen N und Reibungskraft Ffr. 3. Wir stellen die Grundgleichung der Dynamik zusammen: 4. Wir projizieren die Grundgleichung der Dynamik auf die Achse n: Von hier aus bestimmen wir die normale Reaktion: Wir bestimmen den Druck des Autos auf der Brücke: Von hier aus können wir die Geschwindigkeit bestimmen entsprechend Nulldruck auf der Brücke (Q = 0): 4

7 Folie
Vorlesung 2 Nach Substitution der gefundenen Werte der Konstanten erhalten wir: Somit kann ein materieller Punkt unter Einwirkung desselben Kräftesystems eine ganze Klasse von Bewegungen ausführen, die durch die Anfangsbedingungen bestimmt sind. Die Ursprungskoordinaten berücksichtigen den Ursprung des Punktes. Die durch die Projektionen gegebene Anfangsgeschwindigkeit berücksichtigt die Auswirkung der Kräfte, die auf den Punkt wirken, bevor er diesen Abschnitt erreicht, auf seine Bewegung entlang des betrachteten Abschnitts der Trajektorie, d. kinematischer Ausgangszustand. Lösung des inversen Problems der Dynamik - Im allgemeinen Fall sind die Bewegungen eines Kraftpunktes, die auf einen Punkt wirken, zeit-, koordinaten- und geschwindigkeitsabhängige Größen. Die Bewegung eines Punktes wird durch ein System von drei Differentialgleichungen zweiter Ordnung beschrieben: Nach deren Integration ergeben sich jeweils sechs Konstanten C1, C2,…., C6: Die Werte der Konstanten C1, C2,… ., C6 werden aus sechs Anfangsbedingungen bei t = 0 gefunden: Lösungsbeispiel 1 inverses Problem: Ein freier materieller Punkt der Masse m bewegt sich unter Einwirkung einer Kraft F, die in Betrag und Betrag konstant ist. ... Im Anfangsmoment war die Geschwindigkeit des Punktes v0 und fiel in Richtung mit der Kraft zusammen. Bestimmen Sie die Bewegungsgleichung eines Punktes. 1. Bilden Sie die Grundgleichung der Dynamik: 3. Verringern Sie die Ordnung der Ableitung: 2. Wählen Sie ein kartesisches Bezugssystem, richten Sie die x-Achse entlang der Kraftrichtung aus und projizieren Sie die Grundgleichung der Dynamik auf diese Achse: oder xyz 4. Trennen Sie die Variablen: 5. Berechnen Sie die Integrale beider Seiten der Gleichung: 6. Wir stellen die Projektion der Geschwindigkeit als Ableitung der Koordinate nach der Zeit dar: 8. Berechnen Sie die Integrale beider Seiten der Gleichung: 7. Trennen Sie die Variablen: 9. Um die Werte der Konstanten C1 und C2 zu bestimmen, verwenden wir die Anfangsbedingungen t = 0, vx = v0, x = x0: Als Ergebnis erhalten wir die Gleichung von uniform Bewegung (entlang der x-Achse): 5

8 rutsche
Allgemeine Anweisungen zur Lösung des direkten und inversen Problems. Lösungsverfahren: 1. Aufstellung der Bewegungsdifferentialgleichung: 1.1. Wählen Sie ein Koordinatensystem - rechteckig (fest) mit unbekannter Bewegungsbahn, natürlich (beweglich) mit bekannter Bewegungsbahn, zum Beispiel ein Kreis oder eine Gerade. Im letzteren Fall kann eine geradlinige Koordinate verwendet werden. Richten Sie den Ursprung an der Anfangsposition des Punktes (bei t = 0) oder an der Gleichgewichtsposition des Punktes aus, falls er vorhanden ist, zB wenn der Punkt vibriert. 6 1.2. Zeichnen Sie einen Punkt an einer Position, die einem beliebigen Zeitpunkt (für t> 0) entspricht, sodass die Koordinaten positiv sind (s> 0, x> 0). In diesem Fall nehmen wir auch an, dass die Projektion der Geschwindigkeit in dieser Position ebenfalls positiv ist. Bei Schwingungen ändert die Projektion der Geschwindigkeit beispielsweise bei der Rückkehr in die Gleichgewichtslage das Vorzeichen. Dabei ist davon auszugehen, dass sich der Punkt zum betrachteten Zeitpunkt von der Gleichgewichtslage entfernt. Diese Empfehlung ist zukünftig wichtig, wenn mit geschwindigkeitsabhängigen Widerstandskräften gearbeitet wird. 1.3. Befreien Sie den Materialpunkt von Verbindungen, ersetzen Sie deren Wirkung durch Reaktionen, fügen Sie aktive Kräfte hinzu. 1.4. Das Grundgesetz der Dynamik in Vektorform aufschreiben, auf ausgewählte Achsen projizieren, die gegebenen oder reaktiven Kräfte in Zeitvariablen, Koordinaten oder Geschwindigkeiten ausdrücken, wenn sie davon abhängen. 2. Lösung von Differentialgleichungen: 2.1. Senken Sie die Ableitung, wenn die Gleichung nicht auf die kanonische (Standard-)Form reduziert wird. zum Beispiel: oder 2.2. Split-Variablen, zum Beispiel: oder 2.4. Berechnen Sie unbestimmte Integrale auf der linken und rechten Seite der Gleichung, zum Beispiel: 2.3. Wenn die Gleichung drei Variablen enthält, ändern Sie die Variablen, zum Beispiel: und teilen Sie dann die Variablen. Kommentar. Statt zu rechnen unbestimmte Integrale Bestimmte Integrale mit variabler Obergrenze können berechnet werden. Die unteren Grenzen stellen die Anfangswerte der Variablen (Anfangsbedingungen) dar. Dann ist eine gesonderte Ermittlung der Konstanten nicht erforderlich, die automatisch in die Lösung eingeht, zum Beispiel: Unter Verwendung der Anfangsbedingungen bspw. t = 0 , vx = vx0, bestimme die Integrationskonstante: 2.5. Drücken Sie die Geschwindigkeit beispielsweise durch die Ableitung der Koordinaten nach der Zeit aus und wiederholen Sie die Abschnitte 2.2 - 2.4. Wenn die Gleichung auf die kanonische Form reduziert wird, die eine Standardlösung hat, wird diese vorgefertigte Lösung verwendet. Aus den Anfangsbedingungen werden noch Integrationskonstanten gefunden. Siehe zum Beispiel Zögern (Vortrag 4, S. 8). Vorlesung 2 (Fortsetzung 2.2)

9 Folie
Vorlesung 2 (Fortsetzung 2.3) Beispiel 2 zur Lösung des inversen Problems: Kraft ist zeitabhängig. Eine Gewichtslast P beginnt sich auf einer glatten horizontalen Fläche unter der Wirkung einer Kraft F zu bewegen, deren Wert proportional zur Zeit ist (F = kt). Bestimmen Sie die von der Last zurückgelegte Strecke in der Zeit t. 3. Bilden Sie die Grundgleichung der Dynamik: 5. Verringern Sie die Ordnung der Ableitung: 4. Projizieren Sie die Grundgleichung der Dynamik auf die x-Achse: oder 7 6. Trennen Sie die Variablen: 7. Berechnen Sie die Integrale beider Seiten von die Gleichung: 9. Stellen wir die Projektion der Geschwindigkeit als zeitliche Ableitung der Koordinate dar: 10. Berechnen Sie die Integrale beider Seiten der Gleichung: 9. Trennen Sie die Variablen: 8. Bestimmen Sie den Wert der Konstanten C1 vom Anfangs Bedingung t = 0, vx = v0 = 0: Als Ergebnis erhalten wir die Bewegungsgleichung (entlang der x-Achse), die den Wert der zurückgelegten Strecke für die Zeit t angibt: 1. Wir wählen einen Bezugssystem ( Kartesische Koordinaten), so dass der Körper eine positive Koordinate hat: 2. Wir nehmen das Bewegungsobjekt als materiellen Punkt (der Körper bewegt sich translatorisch), lösen es aus der Verbindung (Bezugsebene) und ersetzen es durch eine Reaktion (normale Reaktion von eine glatte Fläche) : 11. Bestimmen Sie den Wert der Konstanten C2 aus der Anfangsbedingung t = 0, x = x0 = 0: Beispiel 3 zur Lösung des inversen Problems: Die Kraft hängt von der Koordinate ab. Ein materieller Punkt der Masse m wird mit einer Geschwindigkeit von v0 von der Erdoberfläche nach oben geschleudert. Die Schwerkraft der Erde ist umgekehrt proportional zum Quadrat der Entfernung von einem Punkt zum Schwerpunkt (dem Erdmittelpunkt). Bestimmen Sie die Abhängigkeit der Geschwindigkeit vom Abstand y zum Erdmittelpunkt. 1. Wir wählen einen Bezugssystem (kartesische Koordinaten), damit der Körper eine positive Koordinate hat: 2. Wir stellen die Grundgleichung der Dynamik zusammen: 3. Wir projizieren die Grundgleichung der Dynamik auf die y-Achse: oder Der Koeffizient von Proportionalität kann anhand des Gewichts eines Punktes auf der Erdoberfläche ermittelt werden: R Daher sieht das Differential der Gleichung aus: oder 4. Verringern Sie die Ordnung der Ableitung: 5. Nehmen Sie die Änderung der Variablen vor: 6. Trennen Sie die Variablen: 7. Berechnen Sie die Integrale beider Seiten der Gleichung: 8. Ersetzen Sie die Grenzwerte: Als Ergebnis erhalten wir den Ausdruck für die Geschwindigkeit als Funktion der y-Koordinate: Die maximale Höhenfluggeschwindigkeit ergibt sich durch die Gleichsetzung der Geschwindigkeit mit Null: Maximale Flughöhe beim Verschwinden des Nenners: Bei der Einstellung von Erdradius und Erdbeschleunigung erhält man also die II. kosmische Geschwindigkeit:

10 Folie
Vorlesung 2 (Fortsetzung 2.4) Beispiel 2 zur Lösung des inversen Problems: Kraft hängt von der Geschwindigkeit ab. Ein Schiff der Masse m hatte eine Geschwindigkeit von v0. Der Widerstand des Wassers gegen die Bewegung des Schiffes ist proportional zur Geschwindigkeit. Bestimmen Sie die Zeit, in der sich die Geschwindigkeit des Bootes nach dem Abstellen des Motors um die Hälfte verringert, sowie die Strecke, die das Boot bis zum vollständigen Stillstand zurücklegt. 8 1. Wir wählen einen Bezugssystem (kartesische Koordinaten), damit der Körper eine positive Koordinate hat: 2. Wir nehmen das Bewegungsobjekt als materiellen Punkt (das Schiff bewegt sich vorwärts), befreien es von Bindungen (Wasser) und ersetzen Sie es durch eine Reaktion (Auftriebskraft - die Kraft von Archimedes) und auch durch die Kraft des Widerstands gegen die Bewegung. 3. Fügen Sie die aktive Kraft (Schwerkraft) hinzu. 4. Bilden Sie die Grundgleichung der Dynamik: 5. Projizieren Sie die Grundgleichung der Dynamik auf die x-Achse: oder 6. Verringern Sie die Ordnung der Ableitung: 7. Trennen Sie die Variablen: 8. Berechnen Sie die Integrale beider Seiten des Gleichung: 9. Ersetze die Grenzen: Man erhält einen Ausdruck, der die Geschwindigkeit und die Zeit t in Beziehung setzt, woraus man die Bewegungszeit bestimmen kann: Die Bewegungszeit, während der die Geschwindigkeit um die Hälfte sinkt: Interessant ist, dass wenn die Geschwindigkeit gegen Null geht, geht die Bewegungszeit gegen unendlich, dh Endgeschwindigkeit kann nicht null sein. Ist das nicht "Perpetuum Motion"? Die zurückgelegte Strecke bis zur Haltestelle ist jedoch der Endwert. Um den zurückgelegten Weg zu bestimmen, wenden wir uns dem Ausdruck zu, den wir nach Herabsetzen der Ordnung der Ableitung erhalten, und nehmen die Änderung der Variablen vor: Nach Integration und Substitution der Grenzen erhalten wir: Den zurückgelegten Weg zum Anschlag: ■ Die Bewegung von ein schräg zum Horizont geworfener Punkt in einem homogenen Schwerefeld ohne Berücksichtigung des Luftwiderstands Eliminiert man die Zeit aus den Bewegungsgleichungen, so erhält man die Flugbahngleichung: Die Flugzeit ergibt sich aus der Gleichsetzung der y-Koordinate mit Null: Die Flugreichweite wird durch Substitution der Flugzeit bestimmt:

11 Folie
Vorlesung 3 Geradlinige Schwingungen eines materiellen Punktes - Die oszillatorische Bewegung eines materiellen Punktes tritt unter der Bedingung auf: Es gibt eine Rückstellkraft, die den Punkt bei jeder Abweichung von dieser Position in die Gleichgewichtslage zurückführt. 9 Es gibt eine Rückstellkraft, eine Gleichgewichtsposition ist stabil Es gibt keine Rückstellkraft, eine Gleichgewichtsposition ist instabil Es gibt keine Rückstellkraft, eine Gleichgewichtsposition ist indifferent. Es ist immer auf die Gleichgewichtslage gerichtet, der Wert ist direkt proportional zur linearen Dehnung (Verkürzung) der Feder, gleich der Abweichung des Körpers von der Gleichgewichtslage: c ist der Koeffizient der Federsteifigkeit, numerisch gleich der Kraft unter dem die Feder ihre Länge um eins ändert, gemessen in N / m im System SI. x y O Schwingungsarten eines Materialpunktes: 1. Freie Schwingungen (ohne Berücksichtigung des Medienwiderstandes). 2. Freie Schwingungen unter Berücksichtigung der Beständigkeit des Mediums (gedämpfte Schwingungen). 3. Erzwungene Schwingungen. 4. Erzwungene Schwingungen unter Berücksichtigung der Beständigkeit des Mediums. ■ Freie Schwingungen - treten nur unter dem Einfluss der Rückstellkraft auf. Schreiben wir das Grundgesetz der Dynamik auf: Wählen wir ein Koordinatensystem, das um die Gleichgewichtsposition (Punkt O) zentriert ist, und projizieren Sie die Gleichung auf die x-Achse: Lassen Sie uns die resultierende Gleichung auf die (kanonische) Standardform reduzieren: Diese Gleichung ist eine homogene lineare Differentialgleichung zweiter Ordnung, deren Lösungsform durch die Wurzeln der Kennlinie bestimmt wird die durch die universelle Substitution erhaltene Gleichung: Die Wurzeln der Kennliniengleichung sind imaginär und gleich: Die allgemeine Lösung der Differentialgleichung hat die Form: Punktgeschwindigkeit: Anfangsbedingungen: Definieren Sie die Konstanten: Die Gleichung der freien Schwingungen hat also die Form: Die Gleichung kann durch einen einzigen Ausdruck dargestellt werden: - die Anfangsphase. Die neuen Konstanten a und - stehen in Beziehung zu den Konstanten C1 und C2 durch die Beziehungen: Bestimmen wir a und: Die Ursache für das Auftreten freier Schwingungen ist die Anfangsverschiebung x0 und / oder die Anfangsgeschwindigkeit v0.

12 Folie
10 Vorlesung 3 (Fortsetzung 3.2) Gedämpfte Schwingungen eines materiellen Punktes - Eine oszillatorische Bewegung eines materiellen Punktes tritt auf, wenn eine Rückstellkraft und eine Bewegungswiderstandskraft vorhanden sind. Die Abhängigkeit der Widerstandskraft gegen Bewegung von der Verschiebung oder Geschwindigkeit wird durch die physikalische Beschaffenheit des Mediums oder der Verbindung bestimmt, die eine Bewegung verhindert. Die einfachste Abhängigkeit ist eine lineare Abhängigkeit von der Geschwindigkeit (viskoser Widerstand): - Viskositätskoeffizient xy O Grundlegende Dynamikgleichung: Projektion der Dynamikgleichung auf die Achse: Bringen wir die Gleichung auf eine Standardform: wobei Die charakteristische Gleichung hat Wurzeln : Die allgemeine Lösung dieser Differentialgleichung hat je nach den Werten der Wurzeln eine andere Form: 1.n< k – случай малого вязкого сопротивления: - корни комплексные, различные. или x = ae-nt x = -ae-nt Частота затухающих колебаний: Период: T* Декремент колебаний: ai ai+1 Логарифмический декремент колебаний: Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени. 2. n >k - bei hohem viskosem Widerstand: - echte Wurzeln, anders. oder - diese Funktionen sind aperiodisch: 3. n = k: - reelle Mehrfachwurzeln. diese Funktionen sind auch aperiodisch:

13 Folie
Vorlesung 3 (Fortsetzung 3.3) Klassifikation von Lösungen freier Schwingungen. Federverbindungsmethoden. Äquivalente Steifigkeit. j j 11 Diff. Gleichung Charakter. Gleichung Roots-Charakter. Gleichungen Lösung einer Differentialgleichung Graph nk n = k

14 rutsche
Vorlesung 4 Erzwungene Schwingungen eines materiellen Punktes - Neben der Rückstellkraft wirkt eine sich periodisch ändernde Kraft, die Störkraft genannt wird. Die Störkraft kann unterschiedlicher Natur sein. Beispielsweise bewirkt die Trägheitswirkung der Unwucht m1 eines rotierenden Rotors im Einzelfall sich harmonisch verändernde Kraftprojektionen: Grundgleichung der Dynamik: Projektion der Dynamikgleichung auf eine Achse: Bringen wir die Gleichung auf die Standardform: 12 Die Lösung dieser inhomogenen Differentialgleichung besteht aus zwei Teilen x = x1 + x2: x1 ist die allgemeine Lösung der entsprechenden homogenen Gleichung und x2 ist die besondere Lösung der inhomogenen Gleichung: Wir wählen die besondere Lösung in der Form der rechten Seite: Die erhaltene Gleichheit muss für jedes t erfüllt sein. Dann: oder So führt der Stoffpunkt bei gleichzeitiger Einwirkung der Rückstell- und Störkräfte eine komplexe Schwingbewegung aus, die sich aus der Addition (Überlagerung) von freien (x1) und erzwungenen (x2) Schwingungen ergibt. Wenn P< k (вынужденные колебания малой частоты), то фаза колебаний совпадает с фазой возмущающей силы: В итоге полное решение: или Общее решение: Постоянные С1 и С2, или a и определяются из начальных условий с использованием полного решения (!): Таким образом, частное решение: Если p >k (erzwungene Schwingungen hoher Frequenz), dann ist die Phase der Schwingungen entgegengesetzt zur Phase der störenden Kraft:

15 Folie
Vorlesung 4 (Fortsetzung 4.2) 13 Dynamischer Koeffizient - das Verhältnis der Amplitude der erzwungenen Schwingungen zur statischen Auslenkung eines Punktes unter der Einwirkung konstante Kraft H = const: Amplitude erzwungener Schwingungen: Statische Abweichung findet sich aus der Gleichgewichtsgleichung: Hier: Also: Also bei p< k (малая частота вынужденных колебаний) коэффициент динамичности: При p >k (hohe Frequenz der erzwungenen Schwingungen) dynamischer Faktor: Resonanz - tritt auf, wenn die Frequenz der erzwungenen Schwingungen mit der Frequenz der Eigenschwingungen übereinstimmt (p = k). Dies tritt am häufigsten beim Starten und Stoppen der Rotation von schlecht ausgewuchteten Rotoren auf, die an elastischen Aufhängungen befestigt sind. Die Differentialgleichung der Schwingungen gleicher Frequenzen: Die jeweilige Lösung in Form der rechten Seite kann nicht genommen werden, da Sie erhalten eine linear abhängige Lösung (siehe allgemeine Lösung). Allgemeine Lösung: Ersetzen in der Differentialgleichung: Nehmen Sie eine bestimmte Lösung in der Form und berechnen Sie die Ableitungen: Damit ergibt sich die Lösung: oder Erzwungene Schwingungen bei Resonanz haben eine Amplitude, die mit der Zeit unbegrenzt ansteigt. Der Einfluss des Bewegungswiderstandes bei erzwungenen Schwingungen. Die Differentialgleichung bei viskosem Widerstand hat die Form: Die allgemeine Lösung wird aus der Tabelle (Vorlesung 3, Seite 11) ausgewählt, abhängig vom Verhältnis von n und k (siehe). Wir nehmen die jeweilige Lösung in die Form und berechnen die Ableitungen: Einsetzen in die Differentialgleichung: Durch Gleichsetzen der Koeffizienten für die gleichen trigonometrischen Funktionen erhalten wir ein Gleichungssystem: Beide Gleichungen potenzieren und zu beiden Gleichungen potenzieren , erhalten wir die Amplitude der erzwungenen Schwingungen: Durch Division der zweiten Gleichung durch die erste erhalten wir die Phasenverschiebung der erzwungenen Schwingungen: So ist die Bewegungsgleichung für erzwungene Schwingungen unter Berücksichtigung des Bewegungswiderstandes z. für n< k (малое сопротивление): Вынужденные колебания при сопротивлении движению не затухают. Частота и период вынужденных колебаний равны частоте и периоду изменения возмущающей силы. Коэффициент динамичности при резонансе имеет конечную величину и зависит от соотношения n и к.

16 rutsche
Vorlesung 5 Relative Bewegung eines materiellen Punktes - Angenommen, das bewegte (nicht inertiale) Koordinatensystem Oxyz bewegt sich nach einem bestimmten Gesetz relativ zum stationären (inertialen) Koordinatensystem O1x1y1z1. Die Bewegung des materiellen Punktes M (x, y, z) relativ zum bewegten System Oxyz ist relativ, relativ zum stationären System O1x1y1z1 ist absolut. Die Bewegung des mobilen Systems Oxyz relativ zum stationären System O1x1y1z1 ist eine tragbare Bewegung. 14 z x1 y1 z1 O1 xy M xyz O Grundgleichung der Dynamik: Absolute Beschleunigung eines Punktes: Absolute Beschleunigung eines Punktes in die Grundgleichung der Dynamik einsetzen: Terme mit Translations- und Coriolisbeschleunigung auf die rechte Seite übertragen: Die übertragenen Terme haben die Dimension von Kräften und gelten als entsprechende Trägheitskräfte, gleich: Dann kann die Relativbewegung eines Punktes als absolut betrachtet werden, wenn wir zu den wirkenden Kräften die translatorischen und Coriolis-Trägheitskräfte addieren: In Projektionen auf die Achse des bewegten Koordinatensystems gilt: Rotation ist gleichförmig, dann εe = 0: 2. Translationale krummlinige Bewegung: Wenn die Bewegung geradlinig ist, dann =: Wenn die Bewegung geradlinig und gleichförmig ist, dann ist das bewegte System träge und die relative Bewegung kann als absolut betrachtet werden: Bewegung (das Relativitätsprinzip der klassischen Mechanik). Einfluss der Erdrotation auf das Gleichgewicht der Körper - Nehmen wir an, der Körper befinde sich auf der Erdoberfläche auf einem beliebigen Breitengrad φ (parallel) im Gleichgewicht. Die Erde dreht sich um ihre Achse von West nach Ost mit einer Winkelgeschwindigkeit: Der Erdradius beträgt etwa 6370 km. S R - volle Reaktion einer nicht glatten Oberfläche. G ist die Schwerkraft der Erde zum Mittelpunkt. Ф - Fliehkraft der Trägheit. Bedingung des relativen Gleichgewichts: Die Resultierende aus Anziehungs- und Trägheitskräften ist die Schwerkraft (Gewicht): Der Betrag der Schwerkraft (Gewicht) auf der Erdoberfläche ist gleich P = mg. Die Fliehkraft ist ein kleiner Bruchteil der Schwerkraft: Auch die Abweichung der Schwerkraft von der Schwerkraftrichtung ist gering: Somit ist der Einfluss der Erdrotation auf das Gleichgewicht der Körper äußerst gering und wird in praktischen Berechnungen nicht berücksichtigt. Der Maximalwert der Trägheitskraft (bei φ = 0 - am Äquator) beträgt nur 0,00343 des Wertes der Schwerkraft

17 Folie
Vorlesung 5 (Fortsetzung 5.2) 15 Einfluss der Erdrotation auf die Bewegung von Körpern im Gravitationsfeld der Erde - Nehmen wir an, der Körper fällt aus einer bestimmten Höhe H über der Erdoberfläche am Breitengrad φ auf die Erde. Wählen wir einen beweglichen Bezugssystem, der starr mit der Erde verbunden ist und die x- und y-Achse tangential zur Parallelen und zum Meridian ausrichtet: Somit wird die Schwerkraft mit der Schwerkraft identifiziert. Darüber hinaus glauben wir, dass die Schwerkraft aufgrund der geringen Auslenkung, wie oben erörtert, senkrecht zur Erdoberfläche gerichtet ist. Die Coriolis-Beschleunigung ist gleich und parallel zur y-Achse nach Westen gerichtet. Die Coriolis-Trägheitskraft ist gleich der entgegengesetzten Richtung. Projizieren wir die Relativbewegungsgleichung auf die Achse: Die Lösung der ersten Gleichung ergibt: Anfangsbedingungen: Die Lösung der dritten Gleichung ergibt: Anfangsbedingungen: Die dritte Gleichung hat die Form: Anfangsbedingungen: Ihre Lösung ergibt: Die erhaltene Lösung zeigt, dass der Körper beim Fallen nach Osten abweicht. Berechnen wir den Wert dieser Abweichung zum Beispiel bei einem Sturz aus 100 m Höhe: Der Zeitpunkt des Sturzes ergibt sich aus der Lösung der zweiten Gleichung: Der Einfluss der Erdrotation auf die Bewegung der Körper ist also extrem klein für praktische Höhen und Geschwindigkeiten und wird in technischen Berechnungen nicht berücksichtigt. Die Lösung der zweiten Gleichung impliziert auch die Existenz einer Geschwindigkeit entlang der y-Achse, die auch die entsprechende Beschleunigung und Coriolis-Trägheitskraft verursachen und verursachen sollte. Der Einfluss dieser Geschwindigkeit und der damit verbundenen Trägheitskraft auf die Bewegungsänderung wird noch geringer sein als die betrachtete Coriolis-Trägheitskraft in Verbindung mit der Vertikalgeschwindigkeit.

18 rutsche
Vorlesung 6 Dynamik eines mechanischen Systems. Ein System materieller Punkte oder ein mechanisches System - Eine Menge materieller oder materieller Punkte, die durch allgemeine Wechselwirkungsgesetze vereint sind (die Position oder Bewegung jedes der Punkte oder eines Körpers hängt von der Position und Bewegung aller anderen ab) Ein System von freien Punkten - deren Bewegung durch keine Verbindungen eingeschränkt ist (z. B. ein Planetensystem , in dem die Planeten als materielle Punkte gelten). Ein System von nicht-freien Punkten oder ein nicht-freies mechanisches System - die Bewegung von materiellen Punkten oder Körpern wird durch die dem System auferlegten Beschränkungen (z. B. ein Mechanismus, eine Maschine usw.) begrenzt. 16 Kräfte, die auf das System wirken. Neben der bisher bestehenden Klassifikation von Kräften (Wirk- und Reaktionskräfte) wird eine neue Klassifikation von Kräften eingeführt: System. 2. Interne Kräfte (i) - Wechselwirkungskräfte zwischen materiellen Punkten oder Körpern, die in diesem System enthalten sind. Ein und dieselbe Kraft kann sowohl eine äußere als auch eine innere Kraft sein. Es hängt alles davon ab, welches mechanische System betrachtet wird. Zum Beispiel: Im System Sonne, Erde und Mond sind alle Gravitationskräfte zwischen ihnen intern. Betrachtet man das System Erde und Mond, so sind die von der Sonne ausgeübten Gravitationskräfte äußere: C З Л Aufgrund des Wirkungs- und Reaktionsgesetzes entspricht jede innere Kraft Fk einer anderen inneren Kraft Fk ', gleich groß und entgegengesetzt in Richtung. Daraus folgen zwei bemerkenswerte Eigenschaften von Schnittgrößen: Der Hauptvektor aller Schnittgrößen des Systems ist gleich Null: Das Hauptmoment aller Schnittgrößen des Systems relativ zu einem beliebigen Mittelpunkt ist gleich Null: Oder in Projektionen auf die Koordinate Achsen: Bemerkung. Obwohl diese Gleichungen den Gleichgewichtsgleichungen ähnlich sind, sind sie es nicht, da auf verschiedene Punkte oder Körper des Systems innere Kräfte aufgebracht werden und diese Punkte (Körper) relativ zueinander bewegen können. Aus diesen Gleichungen folgt, dass die inneren Kräfte die Bewegung des betrachteten Systems als Ganzes nicht beeinflussen. Der Massenschwerpunkt des Systems materieller Punkte. Um die Bewegung des Gesamtsystems zu beschreiben, wird ein geometrischer Punkt eingeführt, der Massenmittelpunkt, dessen Radiusvektor durch den Ausdruck bestimmt wird, wobei M die Masse des Gesamtsystems ist: Oder in Projektionen auf die Koordinate Achsen: Die Formeln für den Massenschwerpunkt ähneln den Formeln für den Schwerpunkt. Der Begriff des Massenschwerpunkts ist jedoch allgemeiner, da er nicht mit Gravitationskräften oder Gravitationskräften zusammenhängt.

19 Folie
Vorlesung 6 (Fortsetzung 6.2) 17 Satz über die Bewegung des Massenschwerpunkts des Systems - Betrachten Sie ein System aus n materiellen Punkten. Wir unterteilen die auf jeden Punkt wirkenden Kräfte in äußere und innere Kräfte und ersetzen sie durch die entsprechenden Resultierenden Fke und Fki. Schreiben wir für jeden Punkt die Grundgleichung der Dynamik auf: oder Summieren wir diese Gleichungen über alle Punkte: Auf der linken Seite der Gleichung führen wir die Massen unter dem Vorzeichen der Ableitung ein und ersetzen die Summe der Ableitungen durch die Ableitung von die Summe: Aus der Definition des Massenmittelpunkts: Setze in die resultierende Gleichung ein: Nach Entfernen der Masse des Systems außerhalb des Vorzeichens der Ableitung erhalten wir oder: Das Produkt aus der Masse des Systems und der Beschleunigung seines Mittelpunkts, die Masse ist gleich dem Hauptvektor der äußeren Kräfte. In Projektionen auf die Koordinatenachsen: Der Massenmittelpunkt des Systems bewegt sich wie ein materieller Punkt mit einer Masse gleich der Masse des Gesamtsystems, auf die alle äußeren auf das System einwirkenden Kräfte wirken. Konsequenzen aus dem Satz über die Bewegung des Massenschwerpunkts des Systems (Erhaltungssätze): 1. Wenn im Zeitintervall der Hauptvektor der äußeren Kräfte des Systems gleich Null ist, Re = 0, dann ist die Geschwindigkeit von der Massenmittelpunkt ist konstant, vC = const (der Massenmittelpunkt bewegt sich gleichmäßig geradlinig - das Gesetz der Erhaltung des Bewegungsschwerpunktes). 2. Wenn im Zeitintervall die Projektion des Hauptvektors der äußeren Kräfte des Systems auf die x-Achse gleich Null ist, Rxe = 0, dann ist die Geschwindigkeit des Massenmittelpunkts entlang der x-Achse konstant, vCx = const (der Massenmittelpunkt bewegt sich gleichmäßig entlang der Achse). Ähnliche Aussagen gelten für die y- und z-Achse. Beispiel: Zwei Personen der Masse m1 und m2 sitzen in einem Boot der Masse m3. Im ersten Moment ruhte das Boot mit den Menschen. Bestimmen Sie die Bewegung des Bootes, wenn sich eine Person mit einem Gewicht von m2 im Abstand a zum Bug des Bootes bewegt hat. 3. Wenn im Zeitintervall der Hauptvektor der äußeren Kräfte des Systems gleich Null ist, Re = 0, und im Anfangsmoment die Geschwindigkeit des Massenmittelpunkts Null ist, vC = 0, dann ist der Radiusvektor von der Massenmittelpunkt bleibt konstant, rC = const (der Massenmittelpunkt ist in Ruhe - das Gesetz der Erhaltung der Lage des Massenmittelpunkts). 4. Wenn im Zeitintervall die Projektion des Hauptvektors der äußeren Kräfte des Systems auf die x-Achse null ist, Rxe = 0, und im Anfangsmoment die Geschwindigkeit des Massenschwerpunkts entlang dieser Achse null ist, vCx = 0, dann bleibt die Koordinate des Massenmittelpunkts entlang der x-Achse konstant, xC = const (der Massenmittelpunkt bewegt sich nicht entlang dieser Achse). Ähnliche Aussagen gelten für die y- und z-Achse. 1. Bewegungsobjekt (Boot mit Menschen): 2. Wir verwerfen Verbindungen (Wasser): 3. Ersetzen Sie die Verbindung durch Reaktion: 4. Fügen Sie aktive Kräfte hinzu: 5. Schreiben Sie den Satz über den Massenschwerpunkt auf: Projizieren Sie auf das x -Achse: O Bestimme, wie weit eine Person der Masse m1 den Sitz vertauschen muss, damit das Boot an Ort und Stelle bleibt: Das Boot bewegt sich um eine Strecke l in die entgegengesetzte Richtung.

20 Folie
Vorlesung 7 Kraftimpuls - ein Maß für die mechanische Wechselwirkung, charakterisiert die Übertragung der mechanischen Bewegung von der Seite der auf einen Punkt wirkenden Kräfte über einen bestimmten Zeitraum: 18 auf den Kraftpunkt im gleichen Zeitintervall: Multiplizieren mit dt: Wir integrieren über ein gegebenes Zeitintervall: Der Bewegungsbetrag eines Punktes ist ein Maß für die mechanische Bewegung, bestimmt durch einen Vektor gleich dem Produkt der Masse eines Punktes durch den Vektor seiner Geschwindigkeit: Satz über die Änderung der Bewegungsbetrag des Systems - Betrachten Sie das System mit n materiellen Punkten. Wir unterteilen die auf jeden Punkt wirkenden Kräfte in äußere und innere Kräfte und ersetzen sie durch die entsprechenden Resultierenden Fke und Fki. Schreiben wir für jeden Punkt die Grundgleichung der Dynamik auf: oder Die Bewegungszahl des Systems materieller Punkte ist die geometrische Summe der Bewegungsbeträge materieller Punkte: Nach Definition des Massenschwerpunkts: Der Vektor des Impulses des Systems ist gleich dem Produkt der Masse des Gesamtsystems durch den Geschwindigkeitsvektor des Massenschwerpunktes des Systems. Dann: In Projektionen auf die Koordinatenachsen: Die Ableitung des Impulsvektors des Systems nach der Zeit ist gleich dem Hauptvektor der äußeren Kräfte des Systems. Fassen wir diese Gleichungen über alle Punkte zusammen: Auf der linken Seite der Gleichung führen wir die Massen unter dem Vorzeichen der Ableitung ein und ersetzen die Summe der Ableitungen durch die Ableitung der Summe: Aus der Definition des Impulses des Systems : In Projektionen auf die Koordinatenachsen:

21 Folie
Satz von Euler - Anwendung des Satzes über die Impulsänderung des Systems auf die Bewegung eines kontinuierlichen Mediums (Wasser). 1. Wir wählen das Wasservolumen im krummlinigen Kanal der Turbine als Bewegungsobjekt: 2. Wir verwerfen die Zwangsbedingungen und ersetzen ihre Wirkung durch Reaktionen (Rпов - Resultierende der Oberflächenkräfte) 3. Addieren Sie aktive Kräfte (Rпов - Resultierende der volumetrischen Kräfte): 4. Schreiben Sie den Satz über die Änderung des Bewegungsbetrages des Systems auf: Der Bewegungsbetrag des Wassers zu den Zeitpunkten t0 und t1 wird dargestellt als die Summe: Änderung des Bewegungsbetrags des Wassers im Zeitintervall: Änderung der Wasserbewegung für ein unendlich kleines Zeitintervall dt:, wobei F1 F2 Aus dem Dichteprodukt, Fläche Kreuzung und Geschwindigkeit pro Sekunde Masse erhalten wir: Setzt man das Differential des Impulses des Systems in den Änderungssatz ein, so erhalten wir: Konsequenzen aus dem Satz über die Impulsänderung des Systems (Erhaltungssätze): 1. Wenn im Zeitintervall der Hauptvektor der äußeren Kräfte des Systems ist gleich Null, Re = 0, dann ist der Impulsvektor konstant, Q = const ist das Gesetz der Impulserhaltung des Systems). 2. Wenn im Zeitintervall die Projektion des Hauptvektors der äußeren Kräfte des Systems auf die x-Achse gleich Null ist, Rxe = 0, dann ist die Projektion des Impulses des Systems auf die x-Achse konstant, Qx = konst. Ähnliche Aussagen gelten für die y- und z-Achse. Vorlesung 7 (Fortsetzung 7.2) Beispiel: Eine Granate der Masse M explodierte mit einer Geschwindigkeit von v in zwei Teile. Die Geschwindigkeit eines der Massefragmente m1 nahm in Bewegungsrichtung auf den Wert v1 zu. Bestimmen Sie die Geschwindigkeit des zweiten Shards. 1. Das Bewegungsobjekt (Granate): 2. Das Objekt ist ein freies System, Verbindungen und deren Reaktionen fehlen. 3. Wirkkräfte addieren: 4. Satz über die Impulsänderung aufschreiben: Auf die Achse projizieren: β Variablen trennen und integrieren: Das rechte Integral ist praktisch Null, da Explosionszeit t

22 rutsche
Vorlesung 7 (Fortsetzung 7.3) 20 Der Drehimpuls eines Punktes oder der Drehimpuls einer Bewegung relativ zu einem bestimmten Zentrum ist ein Maß für die mechanische Bewegung, bestimmt durch einen Vektor gleich dem Vektorprodukt des Radiusvektors eines materiellen Punktes durch die Vektor seines Impulses: Das kinetische Moment eines Systems materieller Punkte relativ zu einem bestimmten Mittelpunkt ist geometrisch die Summe der Momente der Anzahl der Bewegungen aller materiellen Punkte relativ zum gleichen Mittelpunkt: In Projektionen auf die Achse: In Projektionen auf die Achse: Der Satz über die Änderung des Drehimpulses des Systems - Betrachten Sie ein System von n materiellen Punkten. Wir unterteilen die auf jeden Punkt wirkenden Kräfte in äußere und innere Kräfte und ersetzen sie durch die entsprechenden Resultierenden Fke und Fki. Schreiben wir für jeden Punkt die Grundgleichung der Dynamik auf: oder Summieren Sie diese Gleichungen über alle Punkte: Ersetzen Sie die Summe der Ableitungen durch die Ableitung der Summe: Der Ausdruck in Klammern ist das Moment des Impulses des Systems. Von hier aus: Wir multiplizieren jeden der Gleichheitsvektoren mit dem Radiusvektor links: Mal sehen, ob es möglich ist, das Vorzeichen der Ableitung außerhalb des Vektorprodukts zu verschieben: Damit erhalten wir: Die Ableitung des Drehimpulses des Systems relativ zu einem Mittelpunkt in der Zeit ist gleich dem Hauptmoment der äußeren Kräfte des Systems relativ zu demselben Mittelpunkt. In Projektionen auf die Koordinatenachsen: Die Ableitung des Drehimpulses des Systems relativ zu einer bestimmten Achse nach der Zeit ist gleich dem Hauptmoment der äußeren Kräfte des Systems relativ zu derselben Achse.

23 rutsche
Vorlesung 8 21 ■ Konsequenzen aus dem Satz über die Änderung des Drehimpulses des Systems (Erhaltungssätze): 1. Ist im Zeitintervall der Vektor des Hauptmoments der äußeren Kräfte des Systems bezüglich eines Zentrums gleich auf Null, MOe = 0, dann der Vektor des Drehimpulses des Systems relativ zur gleichen Zentrumskonstante, KO = const ist der Erhaltungssatz des Drehimpulses des Systems). 2. Ist im Zeitintervall das Hauptmoment der äußeren Kräfte des Systems relativ zur x-Achse gleich Null, Mxe = 0, dann ist der Drehimpuls des Systems relativ zur x-Achse konstant, Kx = const. Ähnliche Aussagen gelten für die y- und z-Achse. 2. Trägheitsmoment eines starren Körpers um die Achse: Das Trägheitsmoment eines materiellen Punktes um die Achse ist gleich dem Produkt der Masse des Punktes mal dem Quadrat des Abstands des Punktes zur Achse. Das Trägheitsmoment eines starren Körpers um eine Achse ist gleich der Summe der Produkte der Masse jedes Punktes mit dem Quadrat des Abstands dieses Punktes von der Achse. ■ Elemente der Trägheitsmomententheorie - Wenn sich ein starrer Körper dreht, ist das Trägheitsmaß (Widerstand gegen Bewegungsänderung) das Trägheitsmoment um die Drehachse. Betrachten wir die grundlegenden Konzepte der Definition und Methoden zur Berechnung der Trägheitsmomente. 1. Das Trägheitsmoment eines materiellen Punktes um die Achse: Beim Übergang von einer diskreten kleinen Masse zu einer unendlich kleinen Masse eines Punktes wird der Grenzwert einer solchen Summe durch das Integral bestimmt: das axiale Trägheitsmoment eines starren Karosserie. Neben dem axialen Trägheitsmoment eines starren Körpers gibt es noch andere Arten von Trägheitsmomenten: das Fliehkraftmoment eines starren Körpers. polares Trägheitsmoment eines starren Körpers. 3. Der Satz über die Trägheitsmomente eines starren Körpers um parallele Achsen - die Formel für den Übergang zu parallelen Achsen: Trägheitsmoment um die ursprüngliche Achse Statische Trägheitsmomente um die ursprünglichen Achsen Masse des Körpers Achsabstand z1 und z2 Also: Wenn die Achse z1 durch den Massenmittelpunkt geht, dann sind die statischen Momente gleich Null:

24 rutsche
Vorlesung 8 (Fortsetzung 8.2) 22 Trägheitsmoment eines homogenen Stabes konstanten Querschnitts um die Achse: xz L Wählen wir das Elementarvolumen dV = Adx im Abstand x: x dx Elementarmasse: Zur Berechnung des Trägheitsmoments um der Mittelachse (durch den Schwerpunkt verlaufend), reicht es aus, die Position der Achse zu ändern und die Integrationsgrenzen (-L / 2, L / 2) einzustellen. Hier demonstrieren wir die Formel für den Übergang zu parallelen Achsen: zС 5. Das Trägheitsmoment eines homogenen Vollzylinders um die Symmetrieachse: H dr r Wählen wir das Elementarvolumen dV = 2πrdrH (dünner Zylinder mit Radius r): Elementare Masse: Hier haben wir die Formel für das Volumen eines Zylinders V = πR2H verwendet. Um das Trägheitsmoment eines hohlen (dicken) Zylinders zu berechnen, genügt es, die Integrationsgrenzen von R1 bis R2 (R2> R1) festzulegen: 6. Trägheitsmoment eines dünnen Zylinders um die Symmetrieachse (t

25 rutsche
Vorlesung 8 (Fortsetzung 8.3) 23 ■ Die Differentialgleichung der Rotation eines starren Körpers um eine Achse: Schreiben wir einen Satz über die Änderung des Drehimpulses eines starren Körpers, der sich um eine feste Achse dreht: Das kinetische Moment eines rotierenden starren Körper ist: Das Moment äußerer Kräfte um die Drehachse ist gleich dem Drehmoment (Reaktionen und Kraft kein Moment Schwerkraft): Ersetze den Drehimpuls und das Drehmoment im Satz Beispiel: Zwei Personen gleichen Gewichts G1 = G2 hängen an ein über einen festen Block geworfenes Seil mit Gewicht G3 = G1 / 4. Irgendwann begann einer von ihnen mit einer Relativgeschwindigkeit u am Seil zu klettern. Bestimmen Sie die Hubgeschwindigkeit jeder der Personen. 1. Bewegungsobjekt auswählen (Block mit Personen): 2. Verbindungen verwerfen (Stützvorrichtung des Blocks): 3. Verbindung durch Reaktionen ersetzen (Lager): 4. Wirkkräfte hinzufügen (Schwerkraft): 5. Aufschreiben der Satz über die Änderung des kinetischen Moments des Systems in Bezug auf die Drehachsen des Blocks: R Da das Moment der äußeren Kräfte gleich Null ist, muss der Drehimpuls konstant bleiben: Zum Anfangszeitpunkt t = 0, es herrschte Gleichgewicht und Kz0 = 0. Nach Beginn der Bewegung einer Person relativ zum Seil begann sich das gesamte System zu bewegen, aber das Drehimpulssystem muss gleich Null bleiben: Kz = 0. Das kinetische Moment von das System ist die Summe der kinetischen Momente der beiden Personen und des Blocks: Hier ist v2 die Geschwindigkeit der zweiten Person, gleich der Geschwindigkeit des Seils, Beispiel: Bestimmen Sie die Periode kleiner freier Schwingungen eines homogenen Stabes der Masse M und Länge l, mit einem Ende an der festen Drehachse aufgehängt. Oder: Bei kleinen Schwingungen sinφ φ: Schwingungsdauer: Trägheitsmoment des Stabes:

26 rutsche
Vorlesung 8 (Fortsetzung 8.4 - Zusatzmaterial) 24 ■ Elementare Theorie eines Kreisels: Ein Kreisel ist ein starrer Körper, der sich um eine materielle Symmetrieachse dreht, wobei einer seiner Punkte bewegungslos ist. Ein freier Kreisel ist so fixiert, dass sein Massenschwerpunkt stationär bleibt und die Drehachse durch den Massenschwerpunkt geht und jede beliebige Position im Raum einnehmen kann, d.h. die Drehachse ändert ihre Lage wie die eigene Drehachse des Körpers bei sphärischer Bewegung. Die Hauptannahme der angenäherten (Elementar-)Theorie des Kreisels ist, dass der Vektor des Drehimpulses (Drehimpuls) des Rotors als entlang seiner eigenen Drehachse gerichtet angenommen wird. Somit wird trotz der Tatsache, dass der Rotor im allgemeinen Fall an drei Rotationen teilnimmt, nur die Winkelgeschwindigkeit seiner eigenen Rotation ω = dφ / dt berücksichtigt. Der Grund dafür ist, dass in der modernen Technologie der Kreiselrotor mit einer Winkelgeschwindigkeit in der Größenordnung von 5000-8000 rad / s (ca eigene Drehachse zehntausendmal kleiner als diese Geschwindigkeit. Die Haupteigenschaft eines freien Gyroskops besteht darin, dass die Rotorachse eine konstante Richtung im Raum in Bezug auf das Trägheits- (stellare) Bezugssystem beibehält (demonstriert durch das Foucaultsche Pendel, das die Schwingebene in Bezug auf die Sterne unverändert lässt, 1852). . Dies folgt aus dem Erhaltungssatz des Drehimpulses relativ zum Massenmittelpunkt des Rotors, sofern die Reibung in den Lagern der Rotoraufhängungsachsen, Außen- und Innenrahmen vernachlässigt wird: Kraftwirkung auf die Achse eines freien Kreisels. Bei der Einwirkung einer Kraft auf die Rotorachse ist das Moment der äußeren Kräfte relativ zum Schwerpunkt ungleich Null: Kraft, und in Richtung des Vektors des Moments dieser Kraft, d.h. schwenkt nicht um die x-Achse (interne Aufhängung), sondern um die y-Achse (externe Aufhängung). Wenn die Kraft beendet ist, bleibt die Rotorachse in der unveränderten Position, die dem letzten Moment der Kraft entspricht, weil ab diesem Zeitpunkt wird das Moment der äußeren Kräfte wieder gleich Null. Bei einer kurzzeitigen Krafteinwirkung (Stoß) ändert die Kreiselachse ihre Position praktisch nicht. Somit verleiht die schnelle Drehung des Rotors dem Kreisel die Fähigkeit, zufälligen Einflüssen entgegenzuwirken, die dazu neigen, die Position der Drehachse des Rotors zu ändern, und behält unter konstanter Krafteinwirkung die Position der Ebene senkrecht zur wirkenden Kraft bei in der die Achse des Rotors liegt. Diese Eigenschaften werden beim Betrieb von Trägheitsnavigationssystemen verwendet.