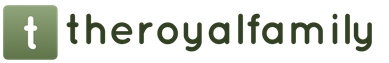Sa është 1 shenjë e barazisë së trekëndëshave. Shenja e parë e barazisë së trekëndëshave. Shenjat e dyta dhe të treta të barazisë së trekëndëshave. Raporti i elementeve në një trekëndësh kënddrejtë

Trekëndësh . Trekëndësha me kënd akut, me kënd të mpirë dhe me kënd të drejtë.

Këmbët dhe hipotenuza. Isosceles dhe trekëndësh barabrinjës.

Shuma e këndeve të një trekëndëshi.

Këndi i jashtëm i trekëndëshit. Shenjat e barazisë së trekëndëshave.

Linja dhe pika të mrekullueshme në trekëndësh: lartësi, mesatare,

përgjysmues, mesatar e pingul, ortocentër,

qendra e gravitetit, qendra e një rrethi të gdhendur, qendra e një rrethi të gdhendur.

Teorema e Pitagorës. Raporti i pamjes në një trekëndësh arbitrar.

Trekëndësh Ashtë një poligon me tre anë (ose tre qoshe). Anët e një trekëndëshi shpesh shënohen me shkronja të vogla, të cilat korrespondojnë me shkronja të mëdha që tregojnë kulme të kundërta.

Nëse të tre qoshet janë të mprehta (Fig. 20), atëherë kjo është trekëndësh me kënd të mprehtë ... Nëse njëri nga qoshet është i drejtë(C, fig. 21), kjo eshte trekëndësh kënddrejtë; partitëa, bqë formojnë një kënd të drejtë quhen këmbët; anësorec, e kundërt kënd i drejtë quhet hipotenuzë... Nëse një nga kënde të mprehta (B, fig. 22), kjo eshte trekëndësh i mpirë.


Trekëndëshi ABC (fig. 23) - barabartës, nëse dy anët e saj janë të barabarta (a= c); këto anë të barabarta quhen anësore, pala e tretë quhet bazë trekëndësh. Trekëndësh ABC (fig. 24) - barabrinjës, nëse te gjitha anët e saj janë të barabarta (a = b = c) Në përgjithësi ( a ≠ b ≠ c) ne kemi shkallën trekëndëshi .

Vetitë themelore të trekëndëshave. Në çdo trekëndësh:

1. Ekziston një kënd më i madh kundrejt anës më të madhe, dhe anasjelltas.

2. Këndet e barabarta shtrihen përballë anëve të barabarta, dhe anasjelltas.

Në veçanti, të gjitha këndet në barabrinjës trekëndëshi është i barabartë.

3. Këndet e një trekëndëshi mblidhen deri në 180 º .

Nga dy vetitë e fundit rezulton se çdo kënd në një barabrinjës

trekëndëshi është 60 º.

4. Duke vazhduar njërën nga brinjët e trekëndëshit (AC, fig. 25), marrim e jashtme

këndi BCD . Këndi i jashtëm i trekëndëshit është i barabartë me shumën e këndeve të brendshme,

jo ngjitur me të : BCD = A + B.

5. Çdo ana e një trekëndëshi është më e vogël se shuma e dy brinjëve të tjera dhe më shumë

dallimet e tyre (a < b + c, a > b – c;b < a + c, b > a – c;c < a + b,c > a – b).

Shenjat e barazisë së trekëndëshave.

Trekëndëshat janë të barabartë nëse janë përkatësisht të barabartë:

a ) dy brinjë dhe këndi ndërmjet tyre;

b ) dy qoshe dhe ana ngjitur me to;

c) tre anët.

Shenjat e barazisë së trekëndëshave me kënd të drejtë.

Dy drejtkëndëshe trekëndëshat janë të barabartë nëse një nga kushtet e mëposhtme është i vërtetë:

1) këmbët e tyre janë të barabarta;

2) këmba dhe hipotenuza e një trekëndëshi janë të barabarta me këmbën dhe hipotenuzën e tjetrit;

3) hipotenuza dhe këndi akut i një trekëndëshi janë të barabartë me hipotenuzën dhe këndin akut të tjetrit;

4) këmba dhe këndi akut ngjitur i një trekëndëshi janë të barabartë me këmbën dhe këndin akut ngjitur të tjetrit;

5) këmba dhe këndi i kundërt akut i një trekëndëshi janë të barabartë me këmbën dhe këndi i kundërt i mprehtë i tjetrit.

Vija dhe pika të mrekullueshme në trekëndësh.

Lartësi trekëndëshi ështëpingul,rënë nga çdo kulm në anën e kundërt ( ose vazhdimi i tij). Kjo anë quhetbaza e trekëndëshit . Tre lartësi të një trekëndëshi ndërpriten gjithmonënë një momenti thirrur ortocentër trekëndësh. Ortocentri i një trekëndëshi me kënd akut (pika O , fig. 26) ndodhet brenda trekëndëshit, dheortocentra e një trekëndëshi të mpirë (pika O , fig. 27) – jashtë; ortocentra e një trekëndëshi kënddrejtë përkon me kulmin e këndit të drejtë.

Mesatare - kjo është seksioni duke lidhur çdo kulm të trekëndëshit me mesin e anës së kundërt. Tre medianë të një trekëndëshi (AD, BE, CF, fig. 28) ndërpriten në një pikë O gjithmonë i shtrirë brenda trekëndëshit dhe duke qenë e tij qendra e gravitetit. Kjo pikë ndan çdo mesatare me një raport 2: 1 nga lart.

Përgjysmues - kjo është segment përgjysmues kënd nga kulmi në një pikë kryqëzim me anën e kundërt. Tre përgjysmues të një trekëndëshi (AD, BE, CF, fig. 29) ndërpriten në një pikë Oh gjithmonë i shtrirë brenda një trekëndëshi dhe duke qenë qendra e rrethit të gdhendur(shih pjesën "Të gdhendurdhe poligonet e përshkruara ").

Përgjysmuesja e ndan anën e kundërt në pjesë proporcionale me anët ngjitur ; për shembull, në fig. 29 AE: CE = AB: BC.

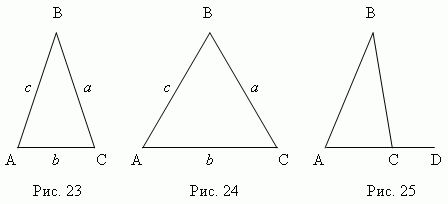
Pingul mesatare Është një pingul i tërhequr nga mesi pikat e segmentit (anët). Tre pingule mesatare të trekëndëshit ABC(KO, MO, JO, fig. 30 ) kryqëzohen në një pikë O, që është qendra rrethi i rrethuar (pikat K, M, N - pikat e mesme të brinjëve të trekëndëshit ABC).

Në një trekëndësh me kënd akut, kjo pikë shtrihet brenda trekëndëshit; në obtuse - jashtë; në formë drejtkëndëshe - në mes të hipotenuzës. Orthocenter, qendra e gravitetit, qendra e rrethuar dhe qendra e rrethit të gdhendur përkojnë vetëm në një trekëndësh barabrinjës.

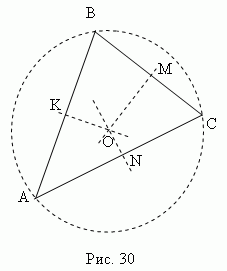
Teorema e Pitagorës. Në një trekëndësh kënddrejtë, katrori i gjatësisëhipotenuza është e barabartë me shumën e katrorëve të gjatësisë së këmbëve.

Prova e teoremës së Pitagorës rrjedh qartë nga Fig. 31. Konsideroni një trekëndësh kënddrejtë ABC me këmbë a, b dhe hipotenuzë c.

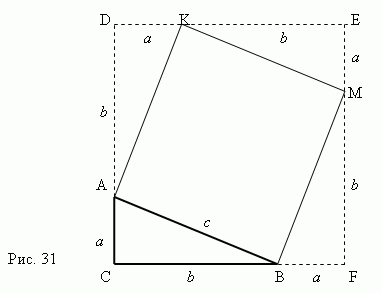
Le të ndërtojmë një shesh AKMB duke përdorur hipotenuzën AB si një anë. Pastajshtrij brinjët e trekëndëshit kënddrejtë ABC pra për të marrë një katror CDEF ana e të cilit është e barabartë mea + bTani është e qartë se sipërfaqja e një katrori CDEF është ( a + b) 2 ... Nga ana tjetër, kjo sipërfaqja është e barabartë me shumën katrore katër trekëndësha kënddrejtë dhe katror AKMB, pra

c 2 + 4 (ab / 2) = c 2 + 2 ab,

nga këtu,

c 2 + 2 ab= (a + b) 2 ,

dhe ne fund kemi:

c 2 =a 2 + b 2 .

Raporti i aspektit në një trekëndësh arbitrar.

Në rastin e përgjithshëm (për një trekëndësh arbitrar) kemi:

c 2 =a 2 + b 2 – 2ab· cos C,

ku C - këndi midis anëvea dhe b .

Dy trekëndësha thuhet se janë të barabartë nëse mund të mbivendosen. Figura 1 tregon trekëndësha të barabartë ABC dhe A 1 B 1 C 1. Secili prej këtyre trekëndëshave mund të mbivendoset në tjetrin në mënyrë që ata të jenë plotësisht të rreshtuar, domethënë, majat dhe anët e tyre do të përputhen në çifte. Shtë e qartë se këndet e këtyre trekëndëshave do të përputhen në çifte.

Kështu, nëse dy trekëndësha janë të barabartë, atëherë elementët (pra, brinjët dhe këndet) e një trekëndëshi janë përkatësisht të barabartë me elementët e trekëndëshit tjetër. Vini re se në trekëndësha të barabartë kundrejt brinjëve përkatësisht të barabarta(d.m.th. mbivendosje) kanë kënde të barabarta, dhe mbrapa: përballë këndeve përkatësisht të barabarta janë brinjët e barabarta.

Kështu, për shembull, në trekëndësha të barabartë ABC dhe A 1 B 1 C 1, të treguar në Figurën 1, anët e barabarta përballë AB dhe A 1 B 1, respektivisht, shtrihen në kënde të barabarta C dhe C 1. Barazia e trekëndëshave ABC dhe А 1 В 1 С 1 do të shënohet si më poshtë: Δ ABC = Δ А 1 В 1 С 1. Rezulton se barazia e dy trekëndëshave mund të vendoset duke krahasuar disa nga elementët e tyre.

Teorema 1. Shenja e parë e barazisë së trekëndëshave. Nëse dy brinjë dhe këndi midis tyre i një trekëndëshi janë respektivisht të barabartë me dy brinjët dhe këndi midis tyre i një trekëndëshi tjetër, atëherë trekëndëshat e tillë janë të barabartë (Fig. 2).

Vërtetim. Konsideroni trekëndëshat ABC dhe A 1 B 1 C 1, për të cilët AB = A 1 B 1, AC = A 1 C 1 ∠ A = ∠ A 1 (shih Fig. 2). Le të vërtetojmë se Δ ABC = Δ A 1 B 1 C 1.

Meqenëse ∠ A = ∠ A 1, atëherë trekëndëshi ABC mund të mbivendoset në trekëndëshin A 1 B 1 C 1 në mënyrë që kulmi A të jetë në një linjë me kulmin A1, dhe brinjët AB dhe AC të mbivendosen, përkatësisht, në rreze. A 1 B 1 dhe A 1 C 1. Meqenëse AB = A 1 B 1, AC = A 1 C 1, ana AB do të rreshtohet me anën A 1 B 1 dhe anën AC - me anën A 1 C 1; në veçanti, pikat B dhe B 1, C dhe C 1 do të kombinohen. Rrjedhimisht, anët BC dhe B 1 C 1 do të kombinohen. Pra, trekëndëshat ABC dhe A 1 B 1 C 1 janë plotësisht të pajtueshëm, që do të thotë se janë të barabartë.

Teorema 2 vërtetohet në mënyrë të ngjashme me metodën e mbivendosjes.

Teorema 2. Shenja e dytë e barazisë së trekëndëshave. Nëse një anë dhe dy kënde ngjitur të një trekëndëshi janë respektivisht të barabartë me brinjën dhe dy këndet ngjitur të një trekëndëshi tjetër, atëherë trekëndëshat e tillë janë të barabartë (Fig. 34).

Komentoni. Teorema 2 përdoret për të vendosur teoremën 3.

Teorema 3. Shuma e çdo dy kënde të brendshme të një trekëndëshi është më e vogël se 180 °.

Teorema 4 rrjedh nga teorema e fundit.

Teorema 4. Këndi i jashtëm i një trekëndëshi është më i madh se çdo kënd i brendshëm që nuk është ngjitur me të.

Teorema 5. Shenja e tretë e barazisë së trekëndëshave. Nëse tre brinjë të një trekëndëshi janë përkatësisht të barabartë me tre brinjë të një trekëndëshi tjetër, atëherë trekëndësha të tillë janë të barabartë ().

Shembulli 1. Në trekëndëshat ABC dhe DEF (fig. 4)

∠ A = ∠ E, AB = 20 cm, AC = 18 cm, DE = 18 cm, EF = 20 cm Krahasoni trekëndëshat ABC dhe DEF. Sa është këndi në trekëndëshin DEF i barabartë me këndin B?

Zgjidhja. Këta trekëndësha janë të barabartë në atributin e parë. Këndi F i trekëndëshit DEF është i barabartë me këndin B të trekëndëshit ABC, pasi këto kënde shtrihen përballë brinjëve të barabarta përkatëse DE dhe AC.

Shembulli 2. Segmentet AB dhe CD (Fig. 5) ndërpriten në pikën O, e cila është mesi i secilit prej tyre. Çfarë është këmba BD nëse këmba AC është 6 m?

Zgjidhja. Trekëndëshat AOC dhe BOD janë të barabartë (sipas kriterit të parë): ∠ AOC = BOD (vertikal), AO = OB, CO = OD (sipas gjendjes).
Barazia e këtyre trekëndëshave nënkupton barazinë e brinjëve të tyre, pra AC = BD. Por meqenëse sipas kushtit AC = 6 m, atëherë BD = 6 m.

Në këtë mësim, ne do të studiojmë shenjën e parë të barazisë së trekëndëshave. Së pari, ne formulojmë dhe vërtetojmë një teoremë mbi kriterin e parë për barazinë e trekëndëshave. Tjetra, ne do të zgjidhim problemet në përdorimin e shenjës së parë të barazisë së trekëndëshave.

Në mësimin e mëparshëm, ne prezantuam konceptin e "trekëndëshave të barabartë" - trekëndësha që mund të kombinohen duke u mbivendosur. Sidoqoftë, është shumë e vështirë të krahasohen figurat sipas përkufizimit, kështu që ne do të prezantojmë shenja të barazisë së trekëndëshave - për disa elementë.

Oriz. 1. Trekëndëshat ABC dhe A 1 B 1 C 1 janë të barabartë

Le të vërtetojmë teoremën: nëse dy brinjë dhe këndi midis tyre i një trekëndëshi dhe dy brinjët përkatëse dhe këndi midis tyre i trekëndëshit të dytë janë të barabartë, atëherë këto trekëndësha janë të barabartë.

Teorema: Jepet. Provoni: ABC dhe.

Vërtetim: Le t'i mbivendosim të dhënat në gjendjen e figurave. Si rezultat i këtij veprimi, kulmet A dhe A 1, segmentet AB dhe A 1 B 1, AC dhe A 1 C 1 përkojnë. Nëse i konsiderojmë trekëndëshat në tërësi, atëherë përkon me.

Teorema vërtetohet.

Le të shqyrtojmë disa detyra.

Segmentet AC dhe BD ndahen me pikën e kryqëzimit të tyre O në gjysmë. Provoje atë.

Vërtetim: Le të bëjmë një vizatim shpjegues.

Oriz. 2. Vizatimi për shembull 1

Vini re se këndet AOB dhe COD janë të barabarta si vertikale, dhe brinjët BO dhe AO të trekëndëshit AOB janë përkatësisht të barabarta me brinjët OD dhe OC të trekëndëshit COD. Prandaj, trekëndëshat AOB dhe COD janë të barabartë në shenjën e parë.

Segmentet AC dhe BD përgjysmohen nga pika e kryqëzimit. Provoje atë.

Oriz. 3. Vizatimi për shembull 2

Në problemin e mëparshëm, ne e vërtetuam atë me kriterin e parë. Nga këto konsiderata, mund të konkludojmë se AB = CD, ∠OAB = ∠OCD.

Tani merrni parasysh trekëndëshat ... Ata kanë AC - një anë e përbashkët, AB = CD, dhe ∠СAB = ∠АCD (siç u vërtetua). Prandaj, sipas kriterit të parë të barazisë. Q.E.D.

Oriz. 4. Vizatim për shembull 3

Në figurën 3, segmentet AB dhe AC janë të barabartë. Këndi 1 është i barabartë me këndin 2. Dihet që AC = 15 cm, DC = 5 cm. Vërtetoni atë. Gjeni gjatësitë e segmenteve të drejtëzave BD dhe AB.

Trekëndëshat janë të barabartë në atributin e parë, sepse ∠1 = ∠2, AB = AC, dhe AD është ana e përbashkët e të dy trekëndëshave. Barazia e trekëndëshave nënkupton barazinë e disa elementeve të tyre përkatëse, pra: BD = CD = 5 cm,

AB = AC = 15 cm.

Përgjigje: 5 cm, 15 cm.

Në Figurën 5, BC = AD. Këndi 1 është i barabartë me këndin 2, AD = 17 cm, CD = 14 cm. Vërtetoni se. Gjeni AB dhe BC.

Oriz. 5. Vizatimi për shembull 4

Trekëndëshi ABC është i barabartë me trekëndëshin CDA. nga shenja e parë. ∠1 = ∠2, CB = AD, dhe AC është ana e përbashkët e të dy trekëndëshave. Nga kjo rrjedh se , .

1. Tema e mësimit "Shenja e parë e barazisë së trekëndëshave"
2. Trekëndësh. Drejtori

1. Nr 36. Butuzov VF, Kadomtsev SB, Prasolova VV. Gjeometria 7 / V.F. Butuzov, S.B. Kadomtsev, V.V. Prasolov, red. Sadovnichy V.A. - M .: Arsimi, 2010.

2. Vërtetoni se trekëndëshat BOA dhe EOC janë të barabartë. Segmentet BE dhe AC përgjysmohen nga pika e kryqëzimit.

3. Vërtetoni se drejtëza që pret segmente të barabarta nga anët e këndit është pingul me përgjysmuesin e saj.

4. * Në anët e këndit M, vizatohen segmente të barabarta MA dhe MS dhe vizatohet përgjysmuesi i tij, mbi të cilin është shënuar pika B. Vërtetoni se BM është përgjysmues i këndit ABC.

Bileta 2

pyetja 1

Teste për barazinë e trekëndëshave (dëshmi e të gjithëve)

Shenja e parë barazia e trekëndëshave: në dy anët dhe këndi midis tyre ( Teorema 3.1. – Shenja e barazisë së trekëndëshave në dy anët dhe këndi midis tyre - Nëse dy anët dhe këndi midis tyre i një trekëndëshi janë të barabartë, përkatësisht, në dy anët dhe këndi midis tyre i një trekëndëshi tjetër, atëherë trekëndësha të tillë janë të barabartë)

Vërtetim:

Le të kenë trekëndëshat ABC dhe A 1 B 1 C 1 këndin A të barabartë me këndin A 1, AB të barabartë me A 1 B 1, AC të barabartë me A 1 C 1, le të vërtetojmë se trekëndëshat janë të barabartë.

Meqenëse A 1 B 1 është e barabartë me A 1 B 2, kulmi B 2 do të përkojë me B 1. Meqenëse këndi B 1 A 1 C 1 është i barabartë me këndin B 2 A 1 C 2, atëherë rrezja A 1 C 2 do të përkojë me A 1 C 1. Meqenëse A 1 C 1 është i barabartë me A 1 C 2, atëherë C 2 përkon me C 1. Pra, trekëndëshi A 1 B 1 C 1 përkon me trekëndëshin A 1 B 2 C 2, që do të thotë se është i barabartë me trekëndëshin ABC Me

Teorema vërtetohet.

2 shenjë barazia e trekëndëshave: përgjatë brinjës dhe këndeve ngjitur me të (teorema 3.2. - Një shenjë e barazisë së trekëndëshave përgjatë një anë dhe këndet ngjitur me të - Nëse ana dhe këndet ngjitur me të të një trekëndëshi janë të barabartë, përkatësisht, në anën dhe këndet ngjitur me të të një trekëndëshi tjetër, atëherë trekëndësha të tillë janë të barabartë)

Vërtetim:

Le te jete ABC dhe A 1 B 1 C 1 janë dy trekëndësha në të cilët AB është i barabartë me A 1 B 1, këndi A është i barabartë me këndin A 1 dhe këndi B është i barabartë me këndin B 1. Le të vërtetojmë se ata janë të barabartë.

Le të jetë A 1 B 2 C 2 një trekëndësh i barabartë me ABC, nga kulmi B 2 në rreze A 1 B 1 dhe kulmi C 2 në të njëjtën gjysmë rrafsh në lidhje me drejtëzën A 1 B 1, ku kulmi C 1 gënjen.

Meqenëse A 1 B 2 është i barabartë me A 1 B 1, atëherë kulmi B 2 përkon me B 1. Meqenëse këndi B 1 A 1 C 2 është i barabartë me këndin B 1 A 1 C 1, dhe këndi A1B1C2 është i barabartë në këndin A1B1C1, atëherë rrezja A 1 C 2 do të përkojë me A 1 C 1, dhe B 1 C 2 do të përkojë me B 1 C 1. Nga kjo rrjedh se kulmi C 2 përkon me C 1. Pra, trekëndëshi A 1 B 1 C 1 përkon me trekëndëshin A 1 B 2 C 2, që do të thotë se është i barabartë me trekëndëshin ABC.

Teorema vërtetohet.

3 shenjë barazia e trekëndëshave: në tre anë (Teorema 3.6. - Shenja e barazisë së trekëndëshave në tre anët - Nëse tre anët e një trekëndëshi janë të barabarta, përkatësisht, në tre anët e një trekëndëshi tjetër, atëherë trekëndësha të tillë janë të barabartë)

Vërtetim:

Le te jete ABC dhe A 1 B 1 C 1 janë dy trekëndësha në të cilët AB është e barabartë me A 1 B 1, AC është e barabartë me A 1 C 1, dhe BC është e barabartë me B 1 C 1. Le të vërtetojmë se ata janë të barabartë.

Le të themi se trekëndëshat nuk janë të barabartë. Atëherë këndi i tyre A nuk është i barabartë me këndin A1, këndi B nuk është i barabartë me këndin B 1 dhe këndi C nuk është i barabartë me këndin C 1. Përndryshe, ata do të ishin të barabartë, sipas atributit të parë.

Le të jetë A 1 B 1 C 2 një trekëndësh i barabartë me trekëndëshin ABC, në të cilin Vertexi C 2 shtrihet në të njëjtin gjysmë rrafsh me kulmin C 1 në raport me drejtëzën A 1 B 1.

Le të jetë D pika mesatare e segmentit С 1 С 2. Trekëndëshat A 1 C 1 C 2 dhe B 1 C 1 C 2 janë dykëndësh me një bazë të përbashkët C 1 C 2. Prandaj, medianat e tyre A 1 D dhe B 1 D janë lartësi, që do të thotë se drejtëzat A 1 D dhe B 1 D janë pingul me drejtëzën C 1 C 2. Drejtëzat A 1 D dhe B 1 D nuk përkojnë, pasi pikat A 1, B 1 , D nuk shtrihen në një vijë të drejtë, por përmes pikës D të drejtëzës С 1 С 2 mund të vizatohet vetëm një drejtëz pingul me të. Ne kemi arritur në një kontradiktë.

Midis numrit të madh të shumëkëndëshave, të cilët në thelb janë një polivijë e mbyllur jo-ndërprerëse, një trekëndësh është forma me numrin më të vogël të këndeve. Me fjalë të tjera, është shumëkëndëshi më i thjeshtë. Por, përkundër gjithë thjeshtësisë së saj, kjo shifër është e mbushur me shumë mistere dhe zbulime interesante, të cilat ndriçohen nga një seksion i veçantë i matematikës - gjeometria. Kjo disiplinë në shkolla fillon të mësohet nga klasa e shtatë, dhe temës "Trekëndëshi" i kushtohet vëmendje e veçantë këtu. Fëmijët jo vetëm që mësojnë rregullat për vetë figurën, por gjithashtu i krahasojnë ato duke studiuar 1, 2 dhe 3 shenja të barazisë së trekëndëshave.

Takimi i parë

Një nga rregullat e para me të cilat njihen nxënësit e shkollës është diçka si kjo: shuma e vlerave të të gjitha këndeve të një trekëndëshi është 180 gradë. Për të konfirmuar këtë, mjafton të matni secilën nga kulmet duke përdorur një raportor dhe të shtoni të gjitha vlerat që rezultojnë. Bazuar në këtë, me dy vlera të njohura, është e lehtë të përcaktohet e treta. Për shembull: Në një trekëndësh, njëri nga këndet është 70 ° dhe tjetri është 85 °, cili është këndi i tretë?

180 - 85 - 70 = 25.

Përgjigje: 25 °.

Detyrat mund të jenë më komplekse nëse tregohet vetëm një vlerë këndi, dhe për vlerën e dytë thuhet vetëm sa ose sa herë është më e madhe ose më pak.

Në një trekëndësh, për të përcaktuar një ose një nga karakteristikat e tij, mund të vizatohen linja të veçanta, secila prej të cilave ka emrin e vet:

• lartësia - një vijë pingul e tërhequr nga maja në anën e kundërt;
• të tre lartësitë, të vizatuara në të njëjtën kohë, kryqëzohen në qendër të figurës, duke formuar një qendër ortoqendër, e cila, në varësi të llojit të trekëndëshit, mund të jetë brenda dhe jashtë;
• mesatare - vija që lidh majën me mesin e anës së kundërt;
• kryqëzimi i medianeve është pika e gravitetit të tij, ndodhet brenda figurës;
• përgjysmues - një vijë që kalon nga kulmi në pikën e kryqëzimit me anën e kundërt, pika e kryqëzimit të tre përgjysmuesve është qendra e rrethit të brendashkruar.

Të vërteta të thjeshta për trekëndëshat

Trekëndëshat, si, në fakt, të gjitha figurat, kanë karakteristikat dhe vetitë e tyre. Siç është përmendur tashmë, kjo figurë është poligoni më i thjeshtë, por me karakteristikat e veta karakteristike:

• një kënd me një vlerë më të madhe qëndron gjithmonë në anën më të gjatë, dhe anasjelltas;
• kënde të barabarta shtrihen përballë anëve të barabarta, një shembull i këtij është një trekëndësh isosceles;
• shuma e këndeve të brendshme është gjithmonë 180 °, e cila tashmë është demonstruar me një shembull;
• kur njëra anë e trekëndëshit shtrihet përtej kufijve të tij, cepi i jashtëm, e cila gjithmonë do të jetë e barabartë me shumën e këndeve që nuk janë ngjitur me të;
• secila anë është gjithmonë më e vogël se shuma e dy anëve të tjera, por më shumë se diferenca e tyre.

Llojet e trekëndëshave

Faza tjetër e njohjes është përcaktimi i grupit të cilit i përket trekëndëshi i paraqitur. Që i përket një specieje ose tjetrës varet nga këndet e trekëndëshit.

• Isosceles - me dy anë të barabarta, të cilat quhen anësore, e treta në këtë rast vepron si baza e figurës. Këndet në bazën e një trekëndëshi të tillë janë të njëjta, dhe mesatarja e tërhequr nga kulmi është përgjysmimi dhe lartësia.
• Një trekëndësh i rregullt ose barabrinjës është ai në të cilin të gjitha brinjët e tij janë të barabarta.
• Drejtkëndëshe: Një nga qoshet e tij është 90 °. Në këtë rast, ana e kundërt me këtë kënd quhet hipotenuzë, dhe dy të tjerat quhen këmbë.
• Trekëndëshi akut - të gjitha këndet më pak se 90 °.
• I mpirë - një nga këndet është më i madh se 90 °.

Barazia dhe ngjashmëria e trekëndëshave

Në procesin e të mësuarit, nuk merret parasysh vetëm një figurë e vetme, por edhe dy trekëndësha krahasohen. Dhe kjo temë në dukje e thjeshtë ka shumë rregulla dhe teorema me të cilat mund të vërtetohet se figurat në fjalë janë trekëndësha të barabartë. Testet e barazisë për trekëndëshat kanë përkufizimin e mëposhtëm: trekëndëshat janë të barabartë nëse brinjët dhe këndet e tyre përkatëse janë të njëjta. Me këtë barazi, nëse i vendosni këto dy figura njëra mbi tjetrën, të gjitha linjat e tyre do të konvergojnë. Gjithashtu, shifrat mund të jenë të ngjashme, në veçanti, kjo vlen për figurat praktikisht identike, që ndryshojnë vetëm në madhësi. Për të nxjerrë një përfundim të tillë për trekëndëshat e paraqitur, duhet të plotësohet një nga kushtet e mëposhtme:

• dy qoshet e një figure janë të barabarta me dy qoshet e një tjetre;
• dy anët e njërës janë proporcionale me dy anët e trekëndëshit të dytë, dhe këndet e formuara nga brinjët janë të barabarta;
• tre anët e figurës së dytë janë të njëjta me të parën.

Sigurisht, për barazinë e padiskutueshme, e cila nuk do të shkaktojë dyshimin më të vogël, është e nevojshme që të ketë vlera të njëjta të të gjithë elementëve të të dy figurave, megjithatë, duke përdorur teorema, problemi thjeshtohet shumë, dhe lejohen vetëm disa kushte për të vërtetuar barazinë e trekëndëshave.

Shenja e parë e barazisë së trekëndëshave

Detyrat në këtë temë zgjidhen bazuar në vërtetimin e një teoreme që tingëllon kështu: "Nëse dy anët e një trekëndëshi dhe këndi që ata formojnë janë të barabartë me dy brinjë dhe këndin e një trekëndëshi tjetër, atëherë figurat janë gjithashtu të barabarta me secilën tjetër."

Si duket prova e teoremës në lidhje me kriterin e parë për barazinë e trekëndëshave? Të gjithë e dinë që dy segmente drejtëzash janë të barabarta nëse janë me të njëjtën gjatësi, ose qarqet janë të barabartë nëse kanë të njëjtën rreze. Dhe në rastin e trekëndëshave, ka disa shenja, me të cilat, mund të supozohet se figurat janë identike, gjë që është shumë e përshtatshme për t'u përdorur kur zgjidhen probleme të ndryshme gjeometrike.

Tingulli i teoremës "Kriteri i parë për barazinë e trekëndëshave" është përshkruar më sipër, por këtu është prova e tij:

• Supozoni se trekëndëshat ABC dhe A 1 B 1 C 1 kanë anët e njëjta AB dhe A 1 B 1 dhe, përkatësisht, BC dhe B 1 C 1, dhe këndet që formohen nga këto anë kanë të njëjtën vlerë, domethënë janë të barabarta Me Pastaj, duke mbivendosur BC ABC në △ А 1 В 1 С 1, marrim koincidencën e të gjitha drejtëzave dhe kulmeve. Nga kjo rrjedh se këta trekëndësha janë absolutisht identikë, që do të thotë se janë të barabartë me njëri-tjetrin.

Teorema "Shenja e parë e barazisë së trekëndëshave" quhet gjithashtu "Në dy anët dhe një kënd". Në fakt, ky është thelbi i tij.

Teorema e kriterit të dytë

Kriteri i dytë i barazisë vërtetohet në mënyrë të ngjashme, prova bazohet në faktin se kur format mbivendosen mbi njëra-tjetrën, ato përputhen plotësisht në të gjitha kulmet dhe anët. Dhe teorema tingëllon kështu: "Nëse njëra anë dhe dy kënde, në formimin e të cilave merr pjesë, korrespondojnë me anën dhe dy qoshet e trekëndëshit të dytë, atëherë këto figura janë identike, domethënë të barabarta".

Shenja dhe prova e tretë

Nëse të dyja shenjat 2 dhe 1 të barazisë së trekëndëshave prekin të dy anët dhe qoshet e figurës, atëherë e treta i referohet vetëm anëve. Pra, teorema ka formulimin e mëposhtëm: "Nëse të gjitha brinjët e një trekëndëshi janë të barabarta me tre brinjët e trekëndëshit të dytë, atëherë figurat janë identike".

Për të vërtetuar këtë teoremë, duhet të thelloheni në vetë përkufizimin e barazisë në më shumë detaje. Në thelb, çfarë do të thotë "trekëndëshat janë të barabartë"? Identiteti sugjeron që nëse mbivendosni një formë mbi tjetrën, të gjithë elementët e tyre do të përkojnë, kjo mund të ndodhë vetëm kur anët dhe këndet e tyre janë të barabarta. Në të njëjtën kohë, këndi përballë njërës nga brinjët, i cili është i njëjtë me atë të trekëndëshit tjetër, do të jetë i barabartë me kulmin përkatës të figurës së dytë. Duhet të theksohet se në këtë pikë prova mund të përkthehet lehtësisht në 1 kriter për barazinë e trekëndëshave. Nëse një sekuencë e tillë nuk respektohet, barazia e trekëndëshave është thjesht e pamundur, përveç atyre rasteve kur figura është një imazh pasqyre i së parës.

Trekëndësha drejtkëndëshe

Në strukturën e trekëndëshave të tillë ka gjithmonë kulme me një kënd prej 90 °. Prandaj, deklaratat e mëposhtme janë të vërteta:

• trekëndëshat me kënde të drejta janë të barabartë nëse këmbët e njërës janë identike me këmbët e së dytës;
• shifrat janë të barabarta nëse hipotenuza e tyre dhe njëra prej këmbëve janë të barabarta;
• trekëndëshat e tillë janë të barabartë nëse këmbët dhe këndi i tyre akut janë identikë.

Kjo veçori i referohet. Për të vërtetuar teoremën, zbatohet aplikimi i figurave në njëra -tjetrën, si rezultat i së cilës trekëndëshat palosen me këmbë në mënyrë që të dalin nga dy vija të drejta me anët CA dhe CA 1.

Përdorim praktik

Në shumicën e rasteve, shenja e parë e barazisë së trekëndëshave përdoret në praktikë. Në fakt, një temë kaq e thjeshtë në dukje e klasës së 7-të për gjeometrinë dhe planimetrinë përdoret gjithashtu për të llogaritur gjatësinë, për shembull, të një kabllo telefoni pa matur terrenin mbi të cilin do të kalojë. Duke përdorur këtë teoremë, është e lehtë të bëhet llogaritjet e nevojshme për të përcaktuar gjatësinë e një ishulli në mes të një lumi pa e kaluar atë. Ose forconi gardhin duke e vendosur shiritin në hapësirë ​​në mënyrë që ta ndajë atë në dy trekëndësha të barabartë, ose të llogaritni elementet komplekse të punës në zdrukthtari, ose kur llogaritni sistemi mahi kulmet gjatë ndërtimit.

Shenja e parë e barazisë së trekëndëshave përdoret gjerësisht në jetën reale "të rritur". Edhe pse në vitet shkollore, kjo temë duket e mërzitshme dhe krejtësisht e panevojshme për shumë njerëz.